题目内容
16.阅读下列材料:x$+\frac{1}{x}$=c$+\frac{1}{c}$的解是x1=c,x2=$\frac{1}{c}$;x-$\frac{1}{x}$=c-$\frac{1}{c}$(即x$+\frac{-1}{x}$=c$+\frac{-1}{c}$的解是x1=c,x2=-$\frac{1}{c}$;
x$+\frac{2}{x}$=c$+\frac{2}{c}$的解是x1=c,x2=$\frac{2}{c}$;
x$+\frac{3}{x}$=c$+\frac{3}{c}$的解是x1=c,x2=$\frac{3}{c}$;
…
(1)请观察上述方程与解的特征,猜想方程x$+\frac{m}{x}$=c$+\frac{m}{c}$(m≠0)的解,并验证你的结论.
(2)利用这个结论解关于x的方程:x$+\frac{2}{x-1}$=a$+\frac{2}{a-1}$.
分析 观察所给式子,可看出:如果方程的左边是未知数与其倒数的倍数的和,方程右边的形式与左边完全相同,只是把其中的未知数换成某个常数,那么这样的方程可直接解得.利用这个结论,可解题.
(1)根据阅读材料得到x1=c,x2=$\frac{m}{c}$.然后将其代入已知方程进行验证即可;
(2)将x+$\frac{2}{x-1}$变形为(x-1)+$\frac{2}{x-1}$=(a-1)+$\frac{2}{a-1}$,求得x-1的值后再来求x的值即可.
解答 解:(1)猜想方程x$+\frac{m}{x}$=c$+\frac{m}{c}$(m≠0)的解是x1=c,x2=$\frac{m}{c}$.
验证:当x=c时,方程x+$\frac{m}{x}$=c+$\frac{m}{c}$成立,当x=$\frac{m}{c}$时,方程x+$\frac{m}{x}$=c+$\frac{m}{c}$成立;
(2)x+$\frac{2}{x-1}$变形为(x-1)+$\frac{2}{x-1}$=(a-1)+$\frac{2}{a-1}$,
x-1=a-1或x-1=$\frac{2}{a-1}$,
∴x=a或x=$\frac{a+1}{a-1}$.
点评 本题考查了解分式方程,需要学生具备观察、比较,猜想、逻辑分析能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知|x+2|+(y-3)2=0,则xy的值为( )
| A. | -6 | B. | 6 | C. | -8 | D. | 8 |
1.用一条长为60cm的绳子围成一个面积为acm2的长方形,a的值不可能为( )
| A. | 240 | B. | 225 | C. | 60 | D. | 30 |
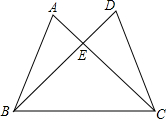 如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.
如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.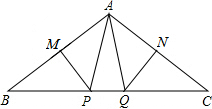 如图所示,∠BAC=120°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.
如图所示,∠BAC=120°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.