题目内容
5.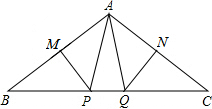 如图所示,∠BAC=120°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.
如图所示,∠BAC=120°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.
分析 由MP和NQ分别垂直平分AB和AC,可得PA=PB,AQ=CQ,即可证得∠B=∠BAP,∠C=∠CAQ,又由∠BAC=120°,可求得∠B+∠C的度数,即可得∠BAP+∠CAQ的度数,继而求得答案.
解答 解:∵PM垂直平分AB,
∴PA=PB,
∴∠B=∠BAP,
同理:QC=QA,
∴∠C=∠CAQ,
∵∠BAC=120°,
∴∠B+∠C=60°,
∴∠BAP+∠CAQ=60°,
∴∠PAQ=∠BAC-∠BAP-∠CAQ=60°.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意求得∠BAP+∠CAQ的度数是关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
15.如果|x-2|=2-x,那么( )
| A. | x<2 | B. | x>2 | C. | x≤2 | D. | x≥2 |
13.同时抛掷两枚质地均匀的硬币,则出现两个正面朝上的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
20. 一张长方形按如图所示的方式折叠,若∠AEB′=30°,则∠B′EF=( )
一张长方形按如图所示的方式折叠,若∠AEB′=30°,则∠B′EF=( )
 一张长方形按如图所示的方式折叠,若∠AEB′=30°,则∠B′EF=( )
一张长方形按如图所示的方式折叠,若∠AEB′=30°,则∠B′EF=( )| A. | 60° | B. | 65° | C. | 75° | D. | 95° |
10.下列长度的三条线段,能组成三角形的是( )
| A. | 1,2,3 | B. | 10,5,4 | C. | 5,2,6 | D. | 2,4,8 |
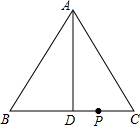 如图,在△ABC中,AB=AC,AD⊥BC于点D,AB=5,AD=4,点P是BC边上的一动点,且不与B、C重合,则点P到AB、AC的距离之和为( )
如图,在△ABC中,AB=AC,AD⊥BC于点D,AB=5,AD=4,点P是BC边上的一动点,且不与B、C重合,则点P到AB、AC的距离之和为( )