题目内容
6.已知分式$\frac{1}{{x}^{2}-1}$无意义,求$\frac{{x}^{2}+6x+9}{x-3}$÷$\frac{x+3}{{x}^{2}-6x+9}$的值.分析 先根据分式无意义的条件,得出x2的值,再化简所求的分式即可.
解答 解:∵分式$\frac{1}{{x}^{2}-1}$无意义,
∴x2-1=0,
解得x2=1,
∴$\frac{{x}^{2}+6x+9}{x-3}$÷$\frac{x+3}{{x}^{2}-6x+9}$=$\frac{(x+3)^{2}}{x-3}$•$\frac{(x-3)^{2}}{x+3}$
=(x+3)(x-3)
=x2-9
=1-9
=-8.
点评 本题考查了分式的化简求值,解答此题的关键是把分式化到最简,然后代值计算.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
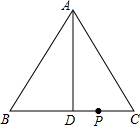 如图,在△ABC中,AB=AC,AD⊥BC于点D,AB=5,AD=4,点P是BC边上的一动点,且不与B、C重合,则点P到AB、AC的距离之和为( )
如图,在△ABC中,AB=AC,AD⊥BC于点D,AB=5,AD=4,点P是BC边上的一动点,且不与B、C重合,则点P到AB、AC的距离之和为( ) 从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.