题目内容
连接下列四边形各边的中点,所得四边形与原四边形相似的是 .(填写序号)

考点:中点四边形,相似多边形的性质
专题:
分析:分别写出各个图形的中点四边形,然后判断与原图形是否相似即可.
解答:解:①顺次连接长宽不等的矩形的各边中点得到的四边形是菱形,不与原图形相;
②顺次连接正方形的各边中点得到的四边形是正方形,与原图形相似;
③顺次连接菱形的各边中点得到的四边形是矩形,不与原图形相似;
④顺次连接等腰梯形的各边中点得到的四边形是菱形,不与原图形相似;
⑤顺次连接直角梯形的各边中点得到的四边形是平行四边形,不与原图形相似;
⑥顺次连接非特殊平行四边形的各边中点得到的四边形是平行四边形,与原图形相似;
故答案为:①⑥.
②顺次连接正方形的各边中点得到的四边形是正方形,与原图形相似;
③顺次连接菱形的各边中点得到的四边形是矩形,不与原图形相似;
④顺次连接等腰梯形的各边中点得到的四边形是菱形,不与原图形相似;
⑤顺次连接直角梯形的各边中点得到的四边形是平行四边形,不与原图形相似;
⑥顺次连接非特殊平行四边形的各边中点得到的四边形是平行四边形,与原图形相似;
故答案为:①⑥.
点评:本题考查了中点四边形和相似多边形的性质,解题的关键是能正确的说出各个图形的中点四边形,难度不大.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
下列各组数中,数值相等的是( )
| A、+32与+22 |
| B、-23与(-2)3 |
| C、-32与(-3)2 |
| D、3×22与(3×2)2 |
关于x的一元二次方程x2+kx-3=0有一个根等于-1,则另一个根等于( )
| A、-2 | B、1 | C、2 | D、3 |
在实数
,-
,-3.14,0,π中,无理数有( )
| 1 |
| 3 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
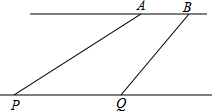 码头A、B位于东西走向的河岸线l上,一游轮在P处测得码头A在其北偏东70°,游轮向东航行10分钟后到达Q处,此时测得码头B在其北偏东35°.已知游轮的速度为30千米/小时,两码头A、B相距2千米.
码头A、B位于东西走向的河岸线l上,一游轮在P处测得码头A在其北偏东70°,游轮向东航行10分钟后到达Q处,此时测得码头B在其北偏东35°.已知游轮的速度为30千米/小时,两码头A、B相距2千米.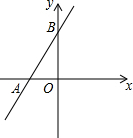 如图,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B(0,4).
如图,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B(0,4).