Question

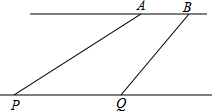码头A、B位于东西走向的河岸线l上，一游轮在P处测得码头A在其北偏东70°，游轮向东航行10分钟后到达Q处，此时测得码头B在其北偏东35°．已知游轮的速度为30千米/小时，两码头A、B相距2千米．
（1）求点P到河岸线l的距离；
（2）若该游轮按原速度从点Q驶向码头B，则它至少需要多长时间才能到达码头B？（参考数据：sin35°≈

3

5

，cos35°≈

4

5

，tan35°≈

7

10

，sin70°≈

9

10

，cos70°≈

7

20

，tan70°≈

27

10

）

Answer 1

考点：解直角三角形的应用-方向角问题

专题：

分析：（1）过点B作BE⊥PQ于E，作BF∥AP交PQ于点F，易证四边形APFB是平行四边形．在△BFQ中，由正弦定理，求出BQ=

7

4

．再在直角△BEQ中，利用三角函数求出BE即可；
（2）由BQ=

7

4

千米，游轮的速度为30千米/小时，根据时间=路程÷速度即可求解．

解答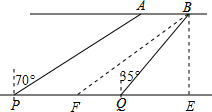：解：（1）过点B作BE⊥PQ于E，作BF∥AP交PQ于点F．
∵AB∥PQ，BF∥AP，
∴四边形APFB是平行四边形，
∴PF=AB=2千米，∠EFB=∠EPA=20°，
∴FQ=PQ-PF=30×

10

60

-2=3（千米）．          
在△BFQ中，∵∠BFQ=20°，∠FQB=90°+35°=125°，
∴∠FBQ=180°-∠BFQ-∠FQB=35°，
由正弦定理得，

BQ

sin∠BFQ

=

FQ

sin∠FBQ

，即

BQ

7 20

=

3

3 5

，
解得BQ=

7

4

．
在Rt△BEQ中，∵∠BEQ=90°，∠QBE=35°，
∴BE=BQ•cos∠QBE≈

7

4

×

4

5

=

7

5

．
答：点P到河岸线l的距离是

7

5

千米；

（2）∵BQ=

7

4

千米，游轮的速度为30千米/小时，
∴该游轮按原速度从点Q驶向码头B的时间为：

7

4

÷30=

7

120

（小时）．
答：若该游轮按原速度从点Q驶向码头B，则它至少需要

7

120

小时才能到达码头B．

点评：本题考查了解直角三角形的应用-方向角问题，平行四边形的判定与性质，正弦定理，锐角三角函数的定义，难度适中．准确作出辅助线利用数形结合是解题的关键．