题目内容
18.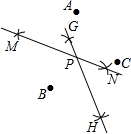 如图所示的是A、B、C、D三点,按如下步骤作图:①先分别以A、B两点为圆心,以大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B、C两点为圆心,以大于$\frac{1}{2}BC$的长为半径作弧,两弧相交于G、H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )
如图所示的是A、B、C、D三点,按如下步骤作图:①先分别以A、B两点为圆心,以大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B、C两点为圆心,以大于$\frac{1}{2}BC$的长为半径作弧,两弧相交于G、H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )| A. | 100° | B. | 120° | C. | 132° | D. | 140° |
分析 根据基本作图可判断MN垂直平分AB,GH垂直平分BC,则点P为△ABC的外心,然后根据圆周角定理可得到∠BPC=2∠BAC.
解答 解:由作法得MN垂直平分AB,GH垂直平分BC,
所以点P为△ABC的外心,
所以∠BPC=2∠BAC=2×66°=132°.
故选C.
点评 本题考查了作图-复杂作图:杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
9.已知等腰三角形的周长为20cm,底边长为y(cm),腰长为x(cm),y与x的函数关系式为y=20-2x,那么自变量x的取值范围是( )
| A. | x>0 | B. | 0<x<10 | C. | 0<x<5 | D. | 5<x<10 |
6.地球上的海洋面积约为361000000千米2,用科学记数法表示为( )
| A. | 3.61×109千米2 | B. | 3.61×108千米2 | C. | 3.61×107千米2 | D. | 3.61×106千米2 |
13. 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )
 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )| A. | ∠1、∠3是同位角 | B. | ∠1、∠2是同旁内角 | C. | ∠1、∠5是同位角 | D. | ∠5、∠6是内错角 |
3.以下列各组数作为三角形的三边长,其中不能构成直角三角形的是( )
| A. | 1,1,$\sqrt{2}$ | B. | 12,16,20 | C. | 1,$\frac{4}{3}$,$\frac{5}{3}$ | D. | 1,2,2 |
10.下列命题中,正确的个数是( )
①若三条线段的比为1:1:$\sqrt{2}$,则它们组成一个等腰直角三角形;
②两条对角线相等的四边形是平行四边形;
③对角线互相平分四边形是平行四边形;
④两个邻角相等的四边形是平行四边形.
①若三条线段的比为1:1:$\sqrt{2}$,则它们组成一个等腰直角三角形;
②两条对角线相等的四边形是平行四边形;
③对角线互相平分四边形是平行四边形;
④两个邻角相等的四边形是平行四边形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.某学习小组中有甲、乙、丙、丁四位同学,为解决尺规作图:“过直线AB外一点M,作一直线垂直于直线AB”,各自提供了如下四种方案,其中正确的是( )
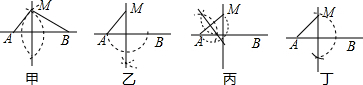
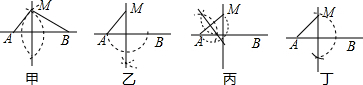
| A. | 甲、乙 | B. | 乙、丙 | C. | 丙、丁 | D. | 甲、乙、丙 |