题目内容
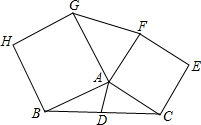 如图,已知AD是△ABC的中线,分别以AB、AC为边向外作正方形,得正方形ABHG和正方形ACEF,求证:
如图,已知AD是△ABC的中线,分别以AB、AC为边向外作正方形,得正方形ABHG和正方形ACEF,求证:(1)GF=2AD;
(2)GF⊥AD.
考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:(1)延长AD至M,使DM=AD,连接BM,根据三角形的中线的定义可得BD=CD,然后利用“边角边”证明△BDM和△CDA全等,根据全等三角形对应边相等可得BM=AC,全等三角形对应角相等可得∠DBM=∠DCA,再根据内错角相等,两直线平行求出AC∥BM,根据两直线平行,同旁内角互补可得∠ABM+∠BAC=180°,然后求出∠ABM=∠GAF,再利用“边角边”证明△ABM和△GAF全等,根据全等三角形对应边相等可得GF=AM;
(2)延长DA与GF相交于点N,根据全等三角形对应角相等可得∠BAM=∠AGF,再求出∠NAG+∠AGN=90°,然后证明即可.
(2)延长DA与GF相交于点N,根据全等三角形对应角相等可得∠BAM=∠AGF,再求出∠NAG+∠AGN=90°,然后证明即可.
解答: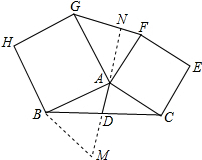 证明:(1)如图,延长AD至M,使DM=AD,连接BM,
证明:(1)如图,延长AD至M,使DM=AD,连接BM,
∵AD是△ABC的中线,
∴BD=CD,
在△BDM和△CDA中,
,
∴△BDM≌△CDA(SAS),
∴BM=AC,∠DBM=∠DCA,
∴AC∥BM,
∴∠ABM+∠BAC=180°,
∵∠BAG=∠CAF=90°,
∴∠GAF+∠BAC=180°,
∴∠ABM=∠GAF,
在△ABM和△GAF中,
,
∴△ABM≌△GAF(SAS),
∴GF=AM,
∴GF=2AD;
(2)延长DA与GF相交于点N,
∵△ABM≌△GAF,
∴∠BAM=∠AGF,
∵∠BAM+∠GAN=180°-90°=90°,
∴∠NAG+∠AGN=90°,
∴AN⊥GF,
故GF⊥AD.
 证明:(1)如图,延长AD至M,使DM=AD,连接BM,
证明:(1)如图,延长AD至M,使DM=AD,连接BM,∵AD是△ABC的中线,
∴BD=CD,
在△BDM和△CDA中,
|
∴△BDM≌△CDA(SAS),
∴BM=AC,∠DBM=∠DCA,
∴AC∥BM,
∴∠ABM+∠BAC=180°,
∵∠BAG=∠CAF=90°,
∴∠GAF+∠BAC=180°,
∴∠ABM=∠GAF,
在△ABM和△GAF中,
|
∴△ABM≌△GAF(SAS),
∴GF=AM,
∴GF=2AD;
(2)延长DA与GF相交于点N,
∵△ABM≌△GAF,
∴∠BAM=∠AGF,
∵∠BAM+∠GAN=180°-90°=90°,
∴∠NAG+∠AGN=90°,
∴AN⊥GF,
故GF⊥AD.
点评:本题考查了全等三角形的判定与性质,正方形的性质,平行线的判定与性质,熟记各性质是解题的关键,难点在于作辅助线构造出全等三角形和直角三角形.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
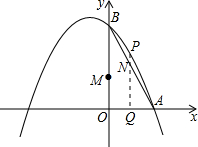 如图,抛物线的对称轴是x=-1,与x轴交于点A(1,0),与y轴交于点 B(0,3).动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
如图,抛物线的对称轴是x=-1,与x轴交于点A(1,0),与y轴交于点 B(0,3).动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒. 如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是
如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是 如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.
如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.