题目内容
 如图所示,AB=CD,BC=DA,∠ABC=∠BCD,求证:AB⊥AC.
如图所示,AB=CD,BC=DA,∠ABC=∠BCD,求证:AB⊥AC.考点:全等三角形的判定与性质
专题:证明题
分析:易证△ABC≌△CDA,可得∠BAC=∠ACD,易证AB∥DC,根据平行线补角和为180°即可解题.
解答:解:∵∠ABC=∠BCD
∴AB∥DC,
在△ABC和△CDA中,
,
∴△ABC≌△CDA,(SSS),
∴∠BAC=∠ACD,
∵AB∥DC,
∴∠BAC+∠ACD=180°,
∴∠BAC=∠ACD=90°,
∴AB⊥AC.
∴AB∥DC,
在△ABC和△CDA中,
|
∴△ABC≌△CDA,(SSS),
∴∠BAC=∠ACD,
∵AB∥DC,
∴∠BAC+∠ACD=180°,
∴∠BAC=∠ACD=90°,
∴AB⊥AC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABC≌△CDA是解题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
A、-
| ||||||||
| B、-7-2×5=-9×5=-45 | ||||||||
C、3÷
| ||||||||
D、-
|
下面是按规律排列的一列数:1、-2、4、-8、16、…其中第7个与第8个数分别为( )
| A、-32,64 |
| B、23,-64 |
| C、-64,128 |
| D、64,-128 |
 如图,在⊙O中,∠BOC=120°,则∠BAC=( )
如图,在⊙O中,∠BOC=120°,则∠BAC=( )| A、120° | B、150° |
| C、60° | D、30° |
 如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.
如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.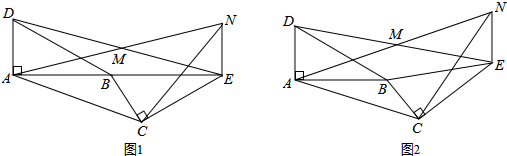
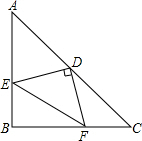 如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于E,交BC为F,
如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于E,交BC为F,