题目内容
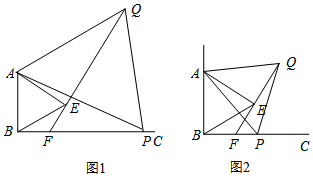
9. 如图,把两个含有45°的三角尺如图放置,∠ECD=ACB=90°,且AB=AE,连接AD交BE于点P,试说明:
如图,把两个含有45°的三角尺如图放置,∠ECD=ACB=90°,且AB=AE,连接AD交BE于点P,试说明:(1)AD=BE;
(2)AD平分∠BAE.
分析 (1)由△ABC和△ECD为含45°的直角三角形,由此即可得出EC=DC、BC=AC,结合∠ECB=∠DCA=90°即可利用全等三角形的判定定理SAS证出△BCE≌△ACD,再根据全等三角形的性质即可得出结论;
(2)由△BCE≌△ACD即可得出∠EBC=∠DAC,根据∠EBC+∠BEC=90°即可得出∠DAC+∠BEC=90°,结合三角形内角和定理即可得出∠APE=90°,再利用等腰三角形的三线合一即可证出AD平分∠BAE.
解答 证明:(1)∵两个含有45°的三角尺如图放置,∠ECD=ACB=90°,
∴EC=DC,BC=AC.
在△BCE和△ACD中,$\left\{\begin{array}{l}{EC=DC}\\{∠ECB=∠DCA=90°}\\{BC=AC}\end{array}\right.$,
∴△BCE≌△ACD(SAS),
∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠EBC=∠DAC.
∵∠EBC+∠BEC=90°,
∴∠DAC+∠BEC=90°,
∴∠APE=90°,即AP⊥BE.
又∵AB=AE,
∴AD平分∠BAE.
点评 本题考查了全等三角形的判定与性质、三角形内角和定义等腰直角三角形以及等腰三角形的性质,解题的关键是:(1)利用全等三角形的判定定理SAS证出△BCE≌△ACD;(2)通过角的计算找出AP⊥BE.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.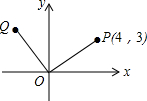 如图所示,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.请求出点Q的坐标.
如图所示,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.请求出点Q的坐标.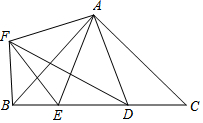 如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,作AF⊥AD,AF=AD,得到△AFB,连接EF.
如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,作AF⊥AD,AF=AD,得到△AFB,连接EF.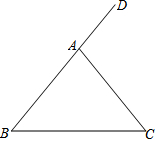 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.