Question

20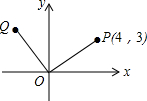．如图所示，点P的坐标为（4，3），把点P绕坐标原点O逆时针旋转90°后得到点Q．请求出点Q的坐标．

Answer 1

分析 作PM⊥x轴于M，QN⊥x轴于N，由旋转的性质得：∠POQ=90°，OQ=OP，由AAS证明△ONQ≌△PMO，得出ON=PM，QN=OM，由点P的坐标为（4，3），得出ON=PM=3，QN=OM=4，即可得出点Q的坐标．

解答 解：作PM⊥x轴于M，QN⊥x轴于N，如图所示：
则∠PMO=∠ONQ=90°，
∴∠P+∠POM=90°，
由旋转的性质得：∠POQ=90°，OQ=OP，
∴∠QON+∠POM=90°，
∴∠QON=∠P，
在△ONQ和△PMO中，$\left\{\begin{array}{l}{∠ONQ=∠PMO}&{\;}\\{∠QON=∠P}&{\;}\\{OQ=PO}&{\;}\end{array}\right.$，
∴△ONQ≌△PMO（AAS），
∴ON=PM，QN=OM，
∵点P的坐标为（4，3），
∴ON=PM=3，QN=OM=4，
∴点Q的坐标为（-3，4）．

点评 本题考查了坐标与图形性质、全等三角形的判定与性质；熟练掌握坐标与图形性质，证明三角形全等是解决问题的关键．