题目内容
19. 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.
分析 直接分别过点E,F作ME∥AB,NF∥AD,利用平行线的性质结合已知表示出:∠AFC和∠AEC的度数,进而得出答案.
解答 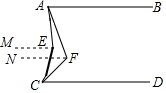 证明:分别过点E,F作ME∥AB,NF∥AD,
证明:分别过点E,F作ME∥AB,NF∥AD,
∵∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,
∴设∠EAF=x,∠ECF=y,
则∠EAB=4x,∠ECD=4y,
故∠BAF=3x,∠DCF=3y,
∵AB∥CD,ME∥AB,NF∥AD,
∴AB∥ME∥NF∥DC,
∴∠BAF=∠AFN=3x,∠BAE=∠AEM=4x,∠MEC=∠ECD=4y,∠NFC=∠FCD=3y,
∴∠AEC=∠AEM+∠MEC=4(x+y),
∠AFC=∠AFN+∠NFC=3(x+y),
∴∠AFC=$\frac{3}{4}$∠AEC.
点评 此题主要考查了平行线的性质,正确作出辅助线是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.“十•一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客a+2.4万人
(2)请判断七天内游客人数最多的是3日;最少的是7日.它们相差2.2万人?
(3)若9月30日的游客人数0.5万人,该景区在10月7号接待了多少游客?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断七天内游客人数最多的是3日;最少的是7日.它们相差2.2万人?
(3)若9月30日的游客人数0.5万人,该景区在10月7号接待了多少游客?
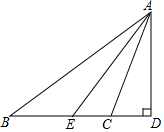 如图所示,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.
如图所示,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线. 如图,把两个含有45°的三角尺如图放置,∠ECD=ACB=90°,且AB=AE,连接AD交BE于点P,试说明:
如图,把两个含有45°的三角尺如图放置,∠ECD=ACB=90°,且AB=AE,连接AD交BE于点P,试说明: