题目内容
8.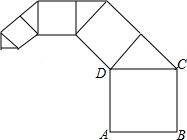 如图,正方形ABCD的边长是2,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2…按此规律继续下去,则S2016的值为($\frac{1}{2}$)2013.
如图,正方形ABCD的边长是2,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2…按此规律继续下去,则S2016的值为($\frac{1}{2}$)2013.
分析 根据题意可知第2个正方形的边长是$\frac{\sqrt{2}}{2}×2$,则第3个正方形的边长是$(\frac{\sqrt{2}}{2})^{2}×2$,…,进而可找出规律,第n个正方形的边长是$(\frac{\sqrt{2}}{2})^{n-1}×2$,那么易求S2016的值.
解答 解:根据题意:第一个正方形的边长为2;
第二个正方形的边长为:$\frac{\sqrt{2}}{2}×2$;
第三个正方形的边长为:$(\frac{\sqrt{2}}{2})^{2}×2$,…
第n个正方形的边长是$(\frac{\sqrt{2}}{2})^{n-1}×2$,
所以S2016的值是($\frac{1}{2}$)2013
故答案为($\frac{1}{2}$)2013
点评 本题考查了正方形的性质、等腰直角三角形的性质、勾股定理.解题的关键是找出第n个正方形的边长.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
19.下列计算正确的是( )
| A. | 2a2-4a2=-2 | B. | 3a+a=3a2 | C. | 5b•b=5b2 | D. | 4a6÷2a3=2a2 |
13.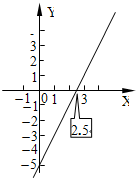 如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
( )
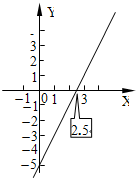 如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是( )
| A. | x>2.5 | B. | x<2.5 | C. | x>-5 | D. | x<-5 |
20.下列运算正确的是( )
| A. | (2x-3)2=4x2+12x-9 | B. | (-3a-2)2=9a2+12a+4 | ||
| C. | (a+b)(a+b)=a2+b2 | D. | (2m+3)(2m-3)=4m2-3 |
18. 在正方形网格中,∠BAC如图所示放置,则cos∠BAC等于( )
在正方形网格中,∠BAC如图所示放置,则cos∠BAC等于( )
 在正方形网格中,∠BAC如图所示放置,则cos∠BAC等于( )
在正方形网格中,∠BAC如图所示放置,则cos∠BAC等于( )| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{3\sqrt{10}}{10}$ | D. | $\frac{\sqrt{10}}{10}$ |