题目内容
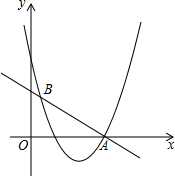 如图,直线y=-
如图,直线y=-| 1 |
| 2 |
| 3 |
| 4 |
(1)k的值是
(2)求抛物线的解析式;
(3)不等式x2+bx+c>-
| 1 |
| 2 |
考点:二次函数与不等式(组),待定系数法求二次函数解析式
专题:
分析:(1)利用图象上点的坐标性质进而得出k的值;
(2)利用待定系数法求出抛物线解析式即可;
(3)利用函数图象进而得出不等式x2+bx+c>-
x+1的解集.
(2)利用待定系数法求出抛物线解析式即可;
(3)利用函数图象进而得出不等式x2+bx+c>-
| 1 |
| 2 |
解答: 解:(1)∵直线y=-
解:(1)∵直线y=-
x+1和抛物线y=x2+bx+c都经过点A(2,0)和点B(k,
),
∴
=-
k+1,
解得:k=
,
故答案为:
;
(2)由(1)得B(
,
),分别将A,B代入y=x2+bx+c得:
,
解得:
,
故抛物线解析式为:y=x2-3x+2;
(3)由图象可得:不等式x2+bx+c>-
x+1的解集是:x<
或x>4.
故答案为:x<
或x>4.
 解:(1)∵直线y=-
解:(1)∵直线y=-| 1 |
| 2 |
| 3 |
| 4 |
∴
| 3 |
| 4 |
| 1 |
| 2 |
解得:k=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
(2)由(1)得B(
| 1 |
| 2 |
| 3 |
| 4 |
|
解得:
|
故抛物线解析式为:y=x2-3x+2;
(3)由图象可得:不等式x2+bx+c>-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:x<
| 1 |
| 2 |
点评:此题主要考查了待定系数法求抛物线解析式以及利用图象判断不等式的解集,正确利用数形结合得出是解题关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
在数0.25,-
,7,0,-3,100中,正数的个数是( )
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
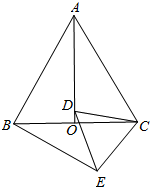 如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.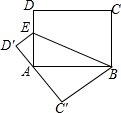 如图,已知点E是长方形ABCD中AD边上一点,将四边形BCDE沿直线BE折叠,折叠后点C的对应点为C′,点D的对应点为D′,若点A在C′D′上,且AB=5,BC=4,则AE=
如图,已知点E是长方形ABCD中AD边上一点,将四边形BCDE沿直线BE折叠,折叠后点C的对应点为C′,点D的对应点为D′,若点A在C′D′上,且AB=5,BC=4,则AE= 如图所示的电路图中,在开关全部断开的情况下,随机闭合开关S1,S2,S3中的两个,则能让两盏灯泡中至少一盏发光的概率为
如图所示的电路图中,在开关全部断开的情况下,随机闭合开关S1,S2,S3中的两个,则能让两盏灯泡中至少一盏发光的概率为
