题目内容
为了估计鱼塘中成品鱼(个体质量在0.5kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如表:
然后做上记号再放回水库中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
(1)请根据表中数据补全如图的直方图(各组中数据包括左端点不包括右端点).

(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).
| 质量/kg | 0.5 | 0.6 | 0.7 | 1.0 | 1.2 | 1.6 | 1.9 |
| 数量/条 | 1 | 8 | 15 | 18 | 5 | 1 | 2 |
(1)请根据表中数据补全如图的直方图(各组中数据包括左端点不包括右端点).

(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).
考点:频数(率)分布直方图,用样本估计总体
专题:图表型
分析:(1)由函数图象可以得出1.1-1.4的有5条,就可以补全直方图;
(2)分别求出各组的频率,就可以得出结论;
(3)由这组数据的个数为50,就可以得出第25个和第26个数的平均数就可以得出结论;
(4)设鱼塘中成品鱼的条数为x,根据作记号的鱼50:x=2:100建立方程求出其解即可.
(2)分别求出各组的频率,就可以得出结论;
(3)由这组数据的个数为50,就可以得出第25个和第26个数的平均数就可以得出结论;
(4)设鱼塘中成品鱼的条数为x,根据作记号的鱼50:x=2:100建立方程求出其解即可.
解答:解:(1)由函数图象可以得出1.1-1.4的有5条,补全图形,得:

(2)由题意,得
0.5-0.8的频率为:24÷50=0.48,
0.8-1.1的频率为:18÷50=0.36,
1.1-1.4的频率为:5÷50=0.1,
1.4-1.7的频率为:1÷50=0.02,
1.7-2.0的频率为:2÷50=0.04.
∵0.48>0.36>0.1>0.04>0.02.
∴估计从鱼塘中随机捕一条成品鱼,其质量落在0.5-0.8的可能性最大;
(3)这组数据的个数为50,就可以得出第25个和第26个数分别是1.0,1.0,
∴(1.0+1.0)÷2=1.0,
鱼塘里质量中等的成品鱼,其质量落在0.8-1.1内;
(4)设鱼塘中成品鱼的条数为x,由题意,得:
50:x=2:100,
解得:x=2500.
2500×
=2260kg.

(2)由题意,得
0.5-0.8的频率为:24÷50=0.48,
0.8-1.1的频率为:18÷50=0.36,
1.1-1.4的频率为:5÷50=0.1,
1.4-1.7的频率为:1÷50=0.02,
1.7-2.0的频率为:2÷50=0.04.
∵0.48>0.36>0.1>0.04>0.02.
∴估计从鱼塘中随机捕一条成品鱼,其质量落在0.5-0.8的可能性最大;
(3)这组数据的个数为50,就可以得出第25个和第26个数分别是1.0,1.0,
∴(1.0+1.0)÷2=1.0,
鱼塘里质量中等的成品鱼,其质量落在0.8-1.1内;
(4)设鱼塘中成品鱼的条数为x,由题意,得:
50:x=2:100,
解得:x=2500.
2500×
| 0.5×1+0.6×8+0.7×15+1×18+1.2×5+1.6×1+1.9×2 |
| 50 |
点评:本题考查了频数分布直方图的运用,比较频率大小的运用,中位数的运用,平均数的运用,由样本数据估计总体数据的运用,解答时认真分析统计表和统计图的数据是关键.

练习册系列答案
相关题目
 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2= 把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为
把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为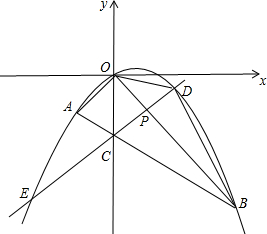 如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,-n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2-2x-3=0的两根.
如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,-n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2-2x-3=0的两根.