题目内容
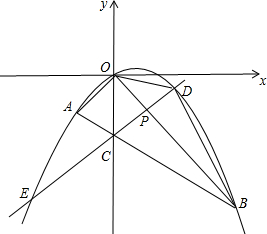 如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,-n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2-2x-3=0的两根.
如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,-n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2-2x-3=0的两根.(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.
考点:二次函数综合题
专题:
分析:(1)首先解方程得出A,B两点的坐标,利用待定系数法确定直线AB和直线OB的解析式即可;
(2)利用待定系数法求出二次函数解析式即可;
(3)利用S△BOD=S△ODQ+S△BDQ得出关于x的二次函数,进而得出最值即可.
(2)利用待定系数法求出二次函数解析式即可;
(3)利用S△BOD=S△ODQ+S△BDQ得出关于x的二次函数,进而得出最值即可.
解答:解(1)解方程x2-2x-3=0,
得 x1=3,x2=-1.
∵m<n,
∴m=-1,n=3
∴A(-1,-1),B(3,-3).
设直线AB的解析式为y=kx+b
∴
,
解得:
,
所以直线AB的解析式为y=-
x-
;
设直线OB的解析式为y=kx,
∴3k=-3,
解得:k=-1,
∴直线OB的解析式为y=-x;
(2)∵抛物线过原点,设抛物线的解析式为y=ax2+bx(a≠0).
∴
,
解得:
,
∴抛物线的解析式为y=-
x2+
x.
(3) △BOD的面积是存在最大值;
△BOD的面积是存在最大值;
过点D作DG⊥x轴,垂足为G,交OB于Q,过B作BH⊥x轴,垂足为H.
设Q(x,-x),D(x,-
x2+
x).
S△BOD=S△ODQ+S△BDQ=
DQ•OG+
DQ•GH,
=
DQ(OG+GH),
=
[x+(-
x2+
x)]×3,
=-
(x-
)2+
,
∵0<x<3,
∴当x=
时,S取得最大值为
,此时D(
,-
).
得 x1=3,x2=-1.
∵m<n,
∴m=-1,n=3
∴A(-1,-1),B(3,-3).
设直线AB的解析式为y=kx+b
∴
|
解得:
|
所以直线AB的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
设直线OB的解析式为y=kx,
∴3k=-3,
解得:k=-1,
∴直线OB的解析式为y=-x;
(2)∵抛物线过原点,设抛物线的解析式为y=ax2+bx(a≠0).
∴
|
解得:
|
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
(3)
 △BOD的面积是存在最大值;
△BOD的面积是存在最大值;过点D作DG⊥x轴,垂足为G,交OB于Q,过B作BH⊥x轴,垂足为H.
设Q(x,-x),D(x,-
| 1 |
| 2 |
| 1 |
| 2 |
S△BOD=S△ODQ+S△BDQ=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 4 |
| 3 |
| 2 |
| 27 |
| 16 |
∵0<x<3,
∴当x=
| 3 |
| 2 |
| 27 |
| 16 |
| 3 |
| 2 |
| 3 |
| 8 |
点评:此题主要考查了二次函数的综合应用以及等腰三角形的性质和三角形面积求法等知识,求面积最值经常利用二次函数的最值求法得出.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
数据:2,5,4,5,3,4,4的众数与中位数分别是( )
| A、4,3 | B、4,4 |
| C、3,4 | D、4,5 |
在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号为偶数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|

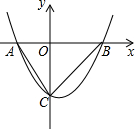 如图所示,二次函数y=x2-x-6的图象交x轴于A、B两点,交y轴于C点.
如图所示,二次函数y=x2-x-6的图象交x轴于A、B两点,交y轴于C点. 如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.
如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.