题目内容
一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球．
（1）求从袋中摸出一个球是黄球的概率；
（2）现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是
，求从袋中取出黑球的个数．
（1）求从袋中摸出一个球是黄球的概率；
（2）现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是
| 1 |
| 3 |
考点：概率公式,分式方程的应用
专题：
分析：（1）由一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球，直接利用概率公式求解即可求得答案；
（2）首先设从袋中取出x个黑球，根据题意得：
=
，继而求得答案．
（2）首先设从袋中取出x个黑球，根据题意得：
| 8-x |
| 20-x |
| 1 |
| 3 |
解答：解：（1）∵一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球，
∴从袋中摸出一个球是黄球的概率为：
=
；
（2）设从袋中取出x个黑球，
根据题意得：
=
，
解得：x=2，
经检验，x=2是原分式方程的解，
所以从袋中取出黑球的个数为2个．
∴从袋中摸出一个球是黄球的概率为：
| 5 |
| 20 |
| 1 |
| 4 |
（2）设从袋中取出x个黑球，
根据题意得：
| 8-x |
| 20-x |
| 1 |
| 3 |
解得：x=2，
经检验，x=2是原分式方程的解，
所以从袋中取出黑球的个数为2个．
点评：此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如图，在△ABC中，点O在AB边上，过点O作BC的平行线交∠ABC的平分线于点D，过点B作BE⊥BD交直线OD于点E．
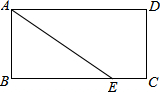如图，在矩形ABCD中，AB=2，AD=4，点E是BC边上的一点，连接AE，若CE=1，求AE的长．
如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=∠BFD．