题目内容
13. 如图所示,PA、PB分别切⊙O于A、B两点,AB交OP于M,N为PM的中点,NT切⊙O于T点,求证:NT=NP.
如图所示,PA、PB分别切⊙O于A、B两点,AB交OP于M,N为PM的中点,NT切⊙O于T点,求证:NT=NP.
分析 直线OP交⊙O于C、D,连接OA,如图,利用切线长定理和切线的性质得到OA⊥PA,PA=PB,OP平分∠APB,根据等腰三角形的性质可判断PO⊥AB,则利用射影定理得到AM2=OM•PM=OM•2MN,再有相交弦定理得到AM2=MD•MC,所以2OM•MN=MD•MC,接着利用切割线定理得到NT2=NC•ND,再利用等量代换得到NT2=MN2,从而得到NT=MN,所以NT=NP.
解答 证明:直线OP交⊙O于C、D,连接OA,如图,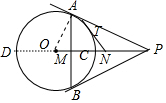
∵PA、PB分别切⊙O于A、B两点,
∴OA⊥PA,PA=PB,OP平分∠APB,
∴PO⊥AB,
∴AM2=OM•PM,
而MN=PN,
∴AM2=OM•2MN,
∵AM2=MD•MC,
∴2OM•MN=MD•MC,
∴NT2=NC•ND=(MN-MC)•(MD+MN)=MN2+(MD-MC)•MN-MC•MD=MN2+2OM•MN-MC•MD=MN2,
∴NT=MN,
∴NT=NP.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.熟练掌握应用射影定理、相交弦定理和切割线是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.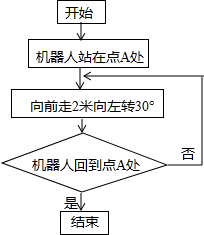 科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
 科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )| A. | 12米 | B. | 16米 | C. | 24米 | D. | 不能确定 |
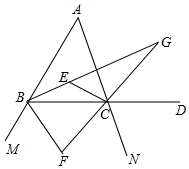 如图,△ABC中,BG平分∠ABC,CE平分∠ACB,延长AB到M,延长AC到N,延长BC到D,BF平分∠DBM,CF平分∠BCN,CG平分∠ACD,已知∠A=68°,分别求∠BEC、∠F、∠G的度数.
如图,△ABC中,BG平分∠ABC,CE平分∠ACB,延长AB到M,延长AC到N,延长BC到D,BF平分∠DBM,CF平分∠BCN,CG平分∠ACD,已知∠A=68°,分别求∠BEC、∠F、∠G的度数.
 如图,AB=AD,∠BAE=∠CAD,∠C=∠E,AC与AE相等吗?
如图,AB=AD,∠BAE=∠CAD,∠C=∠E,AC与AE相等吗?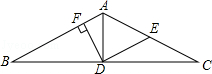 如图,在△ABC中,AB=AC,AD是△ABC的中线,E是AC的中点,连接DE,DF⊥AB于F.求证:
如图,在△ABC中,AB=AC,AD是△ABC的中线,E是AC的中点,连接DE,DF⊥AB于F.求证: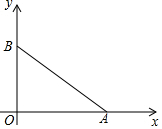 如图,在平面直角坐标系xOy中,已知点(4,0),B(0,3),若有一个直角三角形与Rt△ABO全等且有一条公共的直角边,试写出这个直角三角形未知顶点的坐标.
如图,在平面直角坐标系xOy中,已知点(4,0),B(0,3),若有一个直角三角形与Rt△ABO全等且有一条公共的直角边,试写出这个直角三角形未知顶点的坐标.