题目内容
3.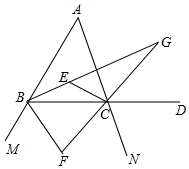 如图,△ABC中,BG平分∠ABC,CE平分∠ACB,延长AB到M,延长AC到N,延长BC到D,BF平分∠DBM,CF平分∠BCN,CG平分∠ACD,已知∠A=68°,分别求∠BEC、∠F、∠G的度数.
如图,△ABC中,BG平分∠ABC,CE平分∠ACB,延长AB到M,延长AC到N,延长BC到D,BF平分∠DBM,CF平分∠BCN,CG平分∠ACD,已知∠A=68°,分别求∠BEC、∠F、∠G的度数.
分析 根据角平分线的性质和三角形内角和定理以及三角形的外角的性质计算即可.
解答 解:∵∠A=68°,
∴∠ABC+∠ACB=112°,
∵BF平分∠ABC,CF平分∠ACB,
∴∠FBC+∠FCB=$\frac{1}{2}$(∠ABC+∠ACB)=56°,
∴∠BEC=124°,
∵∠MBC+∠ABC+∠NCB+∠ACB=360°,
又∵∠ABC+∠ACB=112°,
∴∠MBC+∠NCB=248°,
∵BF、CF分别平分∠MBC、∠NCB,
∴∠FBC+∠FCB=124°,
∴∠F=56°,
∵∠ACD=∠A+∠ABC,
∠GCD=∠G+∠GBC,
又∵GC平分∠ACD,
∴∠G=$\frac{1}{2}$∠A=34°,
点评 本题考查的是三角形的内角和定理,掌握三角形的内角和等于180°是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
14.点A(-1,3)和点B(-1,-1),则A,B相距( )
| A. | 4个单位长度 | B. | 12个单位长度 | C. | 10个单位长度 | D. | 8个单位长度 |
15.某零件厂准备生产2000个零件,甲车间独立生产了一半后,由于要尽快投入市场,乙车间也加入了该零件的生产,乙车间每天生产的零件是甲车间的1.5倍,结果用14天完成了任务,甲车间每天生产零件多少个?
12.若△ABC的两边长为4和5,则能使△ABC是直角三角形的第三边的平方是( )
| A. | 9 | B. | 41 | C. | 3 | D. | 9或41 |
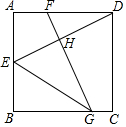 已知:如图,正方形ABCD中,E是AB上一点,FG⊥DE于点H.
已知:如图,正方形ABCD中,E是AB上一点,FG⊥DE于点H. 在如图所示的直角坐标系中描出下列各点:
在如图所示的直角坐标系中描出下列各点: 如图所示,PA、PB分别切⊙O于A、B两点,AB交OP于M,N为PM的中点,NT切⊙O于T点,求证:NT=NP.
如图所示,PA、PB分别切⊙O于A、B两点,AB交OP于M,N为PM的中点,NT切⊙O于T点,求证:NT=NP.