题目内容
5.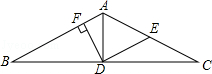 如图,在△ABC中,AB=AC,AD是△ABC的中线,E是AC的中点,连接DE,DF⊥AB于F.求证:
如图,在△ABC中,AB=AC,AD是△ABC的中线,E是AC的中点,连接DE,DF⊥AB于F.求证:(1)∠B=∠EDC;
(2)∠BDF=∠ADE.
分析 (1)根据等腰三角形的性质得到∠BAD=∠CAD,∠ADB=∠ADC=90°,即可得到结论;
(2)根据等腰三角形的判定定理得到∠CAD=∠ADE.根据余角的性质得到∠BAD=∠BDF,等量代换即可得到结论.
解答 证明:(1)∵AB=AC,
∴∠B=∠C,
∵AD是△ABC点的中线,
∴∠ADB=∠ADC=90°,
∵E是AC的中点,
∴DE=AE=EC,
∴∠C=∠EDC,
∴∠B=∠EDC;
(2)∵AE=DE,
∴∠CAD=∠ADE.
在Rt△ABD中,∠ADB=90°,
∴∠B+∠BAD=90°.
∵DF⊥AB,
∴∠B+∠BDF=90°,
∴∠BAD=∠BDF,
∴∠BDF=∠CAD,
∴∠BDF=∠ADE.
点评 本题考查了等腰直角三角形的性质,余角的性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
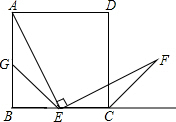 如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG. 如图所示,PA、PB分别切⊙O于A、B两点,AB交OP于M,N为PM的中点,NT切⊙O于T点,求证:NT=NP.
如图所示,PA、PB分别切⊙O于A、B两点,AB交OP于M,N为PM的中点,NT切⊙O于T点,求证:NT=NP.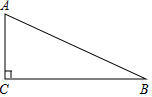 已知△ABC中,∠C=90°,AC=8cm,AB=17cm.
已知△ABC中,∠C=90°,AC=8cm,AB=17cm.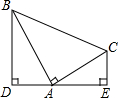 如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足为D,E,
如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足为D,E,