题目内容
1.计算:(1)$\frac{{x}^{2}}{x-1}$+$\frac{x}{1-x}$;
(2)1-$\frac{a-1}{a}$÷$\frac{a-1}{{a}^{2}+2a}$.
分析 (1)原式变形后,利用同分母分式的减法法则计算即可得到结果;
(2)原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=$\frac{{x}^{2}}{x-1}$-$\frac{x}{x-1}$=$\frac{x(x-1)}{x-1}$=x;
(2)原式=1-$\frac{a-1}{a}$•$\frac{a(a+2)}{a-1}$=1-(a+2)=-a-1.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{25}$=±5 | B. | -$\sqrt{0.64}$=0.8 | C. | ±$\sqrt{0.81}$=±0.9 | D. | -$\sqrt{49}$=±7 |
11.若分$\frac{x+y}{2xy}$中的x、y的值都变为原来的3倍,则此分式的值( )
| A. | 不变 | B. | 是原来的3倍 | C. | 是原来的$\frac{1}{3}$ | D. | 是原来的一半 |
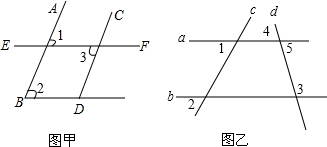 (1)如图甲:∠1=∠2=∠3,完成说理过程并注明理由:
(1)如图甲:∠1=∠2=∠3,完成说理过程并注明理由: