题目内容
7.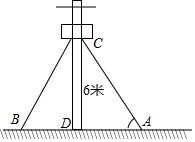 如图,在离地面6m的C处引拉线CB,CA固定电线杆,CA=CB,CD⊥AB于点D,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD.
如图,在离地面6m的C处引拉线CB,CA固定电线杆,CA=CB,CD⊥AB于点D,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD.
分析 在直角△ACD中,已知锐角的度数,以及直角边CD的长,利用三角函数即可求得AC与AD的长.
解答 解:在直角△ACD中,
∵∠CAD=60°,CD=6米,
∴AC=$\frac{CD}{sin60°}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$(m),AD=$\frac{CD}{tan60°}$=$\frac{6}{\sqrt{3}}$=2$\sqrt{3}$(m).
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
18.已知A、B在数轴上分别表示a、b.
(1)对照数轴填写表格:
(2)若A、B两点间的距离记为d,试问d和a、b(a<b)有何数量关系;
(3)求出数轴上到7和-7的距离之和为14的所有整数的和;
(4)若点C表示的数为x,当点C在什么位置时,|x+1|+|x-2|取得的值最小.
(5)动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动.运动到3秒时,两点相距15个单位长度.已知动点A、B的速度之比是3:2(速度单位:1个单位长度/秒).求两个动点运动的速度.
(1)对照数轴填写表格:
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 0 |
(3)求出数轴上到7和-7的距离之和为14的所有整数的和;
(4)若点C表示的数为x,当点C在什么位置时,|x+1|+|x-2|取得的值最小.
(5)动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动.运动到3秒时,两点相距15个单位长度.已知动点A、B的速度之比是3:2(速度单位:1个单位长度/秒).求两个动点运动的速度.
2.已知x1、x2是一元二次方程x2-2x=0的两根,则x1•x2的值是( )
| A. | 0 | B. | 2 | C. | -2 | D. | 4 |
12.下列各式中,运算结果为负数的是( )
| A. | (-2)2 | B. | (-2)3 | C. | (-2)-(-3) | D. | (-2)×(-3) |
19.多项式-2(x-2)去括号得( )
| A. | -2x-2 | B. | -2x+2 | C. | -2x-4 | D. | -2x+4 |