题目内容
已知(a2+b2+1)(a2+b2)-6=0,求a2+b2的值.
考点:换元法解一元二次方程
专题:
分析:设a2+b2=λ,将所给的方程变为λ2+λ-6=0,求得λ值问题即可解决.
解答:解:∵(a2+b2+1)(a2+b2)-6=0,
∴(a2+b2)2+(a2+b2)-6=0,
设a2+b2=λ,则该方程变为λ2+λ-6=0,
解得:λ=3或-2,
即a2+b2=3或-2(舍去).
∴a2+b2的值为3.
∴(a2+b2)2+(a2+b2)-6=0,
设a2+b2=λ,则该方程变为λ2+λ-6=0,
解得:λ=3或-2,
即a2+b2=3或-2(舍去).
∴a2+b2的值为3.
点评:该题主要考查了用换元法来解一元二次方程的问题;解题的关键是科学设元,正确化简,准确计算.

练习册系列答案
相关题目
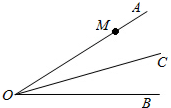 如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10cm,现要在OC、OA上分别找点Q、N,使QM+QN最小,则其最小值是
如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10cm,现要在OC、OA上分别找点Q、N,使QM+QN最小,则其最小值是