题目内容
已知a2-2a-3=0，则a2-2a的值为 ，a3-3a2+5a+4的值为 ．
考点：因式分解的应用
专题：
分析：由已知条件a2-2a-3=0，直接得到a2-2a=3；将a3-3a2+5a+4变形为a（a2-2a）-（a2-2a）+3a+4，根据a2-2a=3，代入化简，即可解决问题．
解答：解：∵a2-2a-3=0，
∴a2-2a=3，a=3或-1；
∴原式
=a（a2-2a）-（a2-2a）+3a+4
=3a-3+3a+4
=6a+1．
当a=3时，原式=19；当a=-1时，原式=-5．
∴a2-2a的值为3，a3-3a2+5a+4的值为19或-5．
∴a2-2a=3，a=3或-1；
∴原式
=a（a2-2a）-（a2-2a）+3a+4
=3a-3+3a+4
=6a+1．
当a=3时，原式=19；当a=-1时，原式=-5．
∴a2-2a的值为3，a3-3a2+5a+4的值为19或-5．
点评：该题主要考查了因式分解在代数式的化简、求值等方面的应用问题；解题的关键是灵活变形、正确化简、准确计算．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
如图，△ABC中，∠A=70°，DO，EO分别为AB，AC的垂直平分线，则∠BOC的度数是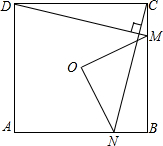
如图，O是正方形ABCD的中心，在正方形ABCD的边BC上任取一点M，过点C作CN⊥DM，交AB于点N，连接OM、ON．求证：