题目内容
5.抛物线y=ax2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表:| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最值为6;③抛物线的对称轴是x=$\frac{1}{2}$;④在对称轴左侧,y随x的增大而增大.
| A. | ①④ | B. | ②③ | C. | ①③④ | D. | ③④ |
分析 根据表中数据和抛物线的对称性,可得到抛物线的开口向下,当x=-1时,y=4,当x=2时,y=4,因此可得抛物线的对称轴是直线x=$\frac{2-1}{2}$=$\frac{1}{2}$,即可得出抛物线与x轴的交点为(-2,0)和(3,0);再根据抛物线的性质即可进行判断.
解答 解:∵当x=-1时,y=4,当x=2时,y=4,
∴抛物线的对称轴是直线x=$\frac{2-1}{2}$=$\frac{1}{2}$;③正确
∴抛物线与x轴的交点为(-2,0)和(3,0);①正确
根据表中数据得到抛物线的开口向下,
∴当x=$\frac{1}{2}$时,函数有最大值,而不是x=0,或1对应的函数值6,②错误
并且在直线x=$\frac{1}{2}$的左侧,y随x增大而增大.④正确
所以①③④正确,②错.
故选:C.
点评 本题考查了抛物线y=ax2+bx+c的性质:抛物线是轴对称图形,它与x轴的两个交点是对称点,对称轴与抛物线的交点为抛物线的顶点;a<0时,函数有最大值,在对称轴左侧,y随x增大而增大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.某次数学趣味竞赛共有10道题目,每道题答对得10分,答错或不答得0分,全班40名同学参加了此次竞赛,他们的得分情况如下表所示
则全班40名同学的成绩的中位数和众数分别是75,70.
| 成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 2 | 5 | 13 | 10 | 7 | 3 |
20.某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可毛获利润共2.7万元.[毛利润=(售价-进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
| 国外品牌 | 国内品牌 | |
| 进价(元/部) | 4400 | 2000 |
| 售价(元/部) | 5000 | 2500 |
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
10.学校篮球集训队11名队员进行定点投篮训练,11名队员在1分钟内投进篮框的球数和人数如下表:
则11名队员投进篮框的球数的中位数是9个.
| 球数/个 | 6 | 7 | 8 | 9 | 10 | 12 |
| 人数 | 1 | 1 | 1 | 4 | 3 | 1 |
17.若关于x的不等式ax+3>0的解集为x<3,则关于m的不等式m+2a<1的解为( )
| A. | m<3 | B. | m<-3 | C. | m>-3 | D. | m>-2 |
14. 如图,数轴上点A、B分别对应实数a、b,则下列结论正确的是( )
如图,数轴上点A、B分别对应实数a、b,则下列结论正确的是( )
 如图,数轴上点A、B分别对应实数a、b,则下列结论正确的是( )
如图,数轴上点A、B分别对应实数a、b,则下列结论正确的是( )| A. | a>b | B. | |a|>|b| | C. | a+b>0 | D. | -a>b |
15. 如图,直线l1与l2相交于点O,OM⊥l1,若α=54°,则β=( )
如图,直线l1与l2相交于点O,OM⊥l1,若α=54°,则β=( )
 如图,直线l1与l2相交于点O,OM⊥l1,若α=54°,则β=( )
如图,直线l1与l2相交于点O,OM⊥l1,若α=54°,则β=( )| A. | 46° | B. | 36° | C. | 45° | D. | 54° |
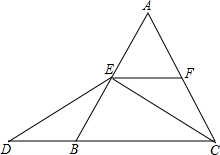 如图,在边长为2的等边△ABC中,E为AB的中点,EF∥BC,交AC于点F,点D为CB延长线上一点,且DE=EC.
如图,在边长为2的等边△ABC中,E为AB的中点,EF∥BC,交AC于点F,点D为CB延长线上一点,且DE=EC.