题目内容
 我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.利用“作差法”解决下列问题:
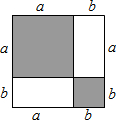
我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.利用“作差法”解决下列问题:(1)如图,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
(2)已知小丽和小颖分别两次购买一种商品,第一次该商品的价格为a元/千克,第二次该商品的价格为b元/千克(a、b是正数,且a≠b),小丽两次都买了m千克商品,两次的平均价格为M,小颖两次都购买n元价格的商品,两次的平均价格为N,你能求出小丽和小颖两次购买商品的平均价格吗?试比较小丽和小颖所购买商品的平均价格的高低.
考点:分式的加减法,完全平方公式
专题:应用题
分析:(1)根据题意,利用正方形及长方形的面积公式表示出M与N,利用作差法判断即可得到结果;
(2)根据题意表示出M与N,利用作差法比较即可.
(2)根据题意表示出M与N,利用作差法比较即可.
解答:解:(1)根据题意得:M=a2+b2,N=2ab,M-N=a2+b2-2ab=(a-b)2,
又∵a≠b,∴(a-b)2>0,
∴M>N;
(2)∵M=
=
,N=
=
,
则M-N=
-
=
=
>0,
∴M>N.
又∵a≠b,∴(a-b)2>0,
∴M>N;
(2)∵M=
| am+bm |
| 2m |
| a+b |
| 2 |
| 2n | ||||
|
| 2ab |
| a+b |
则M-N=
| a+b |
| 2 |
| 2ab |
| a+b |
| (a+b)2-4ab |
| 2(a+b) |
| (a-b)2 |
| 2(a+b) |
∴M>N.
点评:此题考查了分式的加减法,以及完全平方公式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是一个以线段AB为直径的半圆,请用圆规和直尺作出一个60°的角,使这个角的顶点在线段AB上.(不要求写作法,但要保留作图痕迹)
如图是一个以线段AB为直径的半圆,请用圆规和直尺作出一个60°的角,使这个角的顶点在线段AB上.(不要求写作法,但要保留作图痕迹)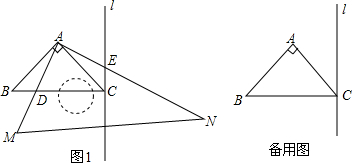
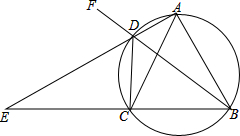 如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,若AB=AC.
如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,若AB=AC.
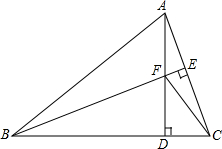 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.