题目内容
9.用换元法解方程$\frac{3x}{{x}^{2}-1}$+$\frac{{x}^{2}-1}{x}$=$\frac{5}{2}$时,若设$\frac{x}{{x}^{2}-1}$=y,则原方程可化为关于y的整式方程为6y2+2=5y.分析 根据设出的y将原方程变形即可.
解答 解:用换元法解方程$\frac{3x}{{x}^{2}-1}$+$\frac{{x}^{2}-1}{x}$=$\frac{5}{2}$时,若设$\frac{x}{{x}^{2}-1}$=y,则原方程可化为关于y的整式方程为3y+$\frac{1}{y}$=$\frac{5}{2}$,
去分母得:6y2+2=5y,
故答案为:6y2+2=5y
点评 此题考查了换元法解分式方程,当分式方程比较复杂时,通常采用换元法使分式方程简化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.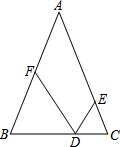 如图,在△ABC中,AB=AC,∠A=40°,CE=CD,BD=BF,则∠EDF的度数为( )
如图,在△ABC中,AB=AC,∠A=40°,CE=CD,BD=BF,则∠EDF的度数为( )
 如图,在△ABC中,AB=AC,∠A=40°,CE=CD,BD=BF,则∠EDF的度数为( )
如图,在△ABC中,AB=AC,∠A=40°,CE=CD,BD=BF,则∠EDF的度数为( )| A. | 40° | B. | 55° | C. | 65° | D. | 70° |

 如图,已知四边形ABCD,其中A(1,1),B(2,2),C(0,3),D(-3,0),作出四边形ABCD关于原点对称的四边形A′B′C′D′.
如图,已知四边形ABCD,其中A(1,1),B(2,2),C(0,3),D(-3,0),作出四边形ABCD关于原点对称的四边形A′B′C′D′.