题目内容
12. 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.(1)求证:AD=OC;
(2)求证:OE是CD的垂直平分线;
(3)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
分析 (1)根据角平分线的性质和HL证明Rt△ODE≌Rt△OCE进行解答即可;
(2)△ODE≌△OCE,可得出OD=OC,DE=CE,利用垂直平分线的性质的逆定理,即可得出OE是CD的垂直平分线;
(2)先根据E是∠AOB的平分线,∠AOB=60°可得出∠AOE=∠BOE=30°,由直角三角形的性质可得出OE=2DE,同理可得出DE=2EF即可得出结论
解答 证明:(1)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,
∴DE=CE,∠EOD=∠EOC,
在Rt△ODE与Rt△OCE中,
$\left\{\begin{array}{l}{DE=CE}\\{OE=OE}\end{array}\right.$,
∴Rt△ODE≌Rt△OCE,
∴OD=OC;
(2)∵Rt△ODE≌Rt△OCE,
∴OD=OC,ED=EC,
∴点O、点E在线段CD的垂直平分线上,
∴OE是CD的垂直平分线;
(3)OE=4EF.
∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
点评 本题考查的是角平分线的性质及直角三角形的性质、等腰三角形的判定与性质,熟知以上知识是解答此题的关键.

练习册系列答案
相关题目
17.一个运动员打尔夫球,若球的飞行高度y(m)与水平距离x(m)之间的函数表达式为y=-$\frac{1}{90}{({x-30})^2}$+10,则高尔夫球第一次落地时距离运动员( )
| A. | 10m | B. | 20m | C. | 30m | D. | 60m |
4.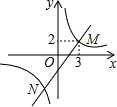 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )| A. | 2,2 | B. | 3,8 | C. | 2,6 | D. | -2,-8 |
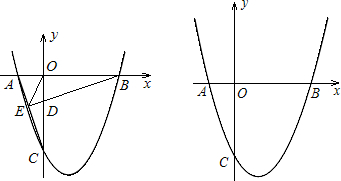
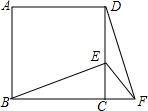 如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.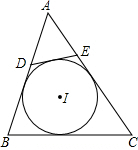 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为9.
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为9. 已知:如图,直线AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,
已知:如图,直线AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,