��Ŀ����
6����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��֪���κ���y=$\frac{1}{2}$x2+bx+c��ͼ�����A��0��-2���͵�B��2��-2�����ҵ�C���B��������ԭ��Գƣ���1����b��c��ֵ�����жϵ�C�Ƿ��ڴ��������ϣ���˵�����ɣ�
��2������PΪ����������һ�㣬������x�ᣬy��ĶԳƵ�ֱ�ΪM��N�����Ƿ����������P��ʹ��M��Nǡ�ö���ֱ��BC�ϣ�����ڣ������P�����꣬�粻���ڣ���˵�����ɣ�
��3������P���Q����ԭ��Գƣ�����P��λ��ֱ��BC�·������������˶�ʱ�����ı���PBQC����������ֵ��
���� ��1����A��0��-2����B��2��-2������y=$\frac{1}{2}$x2+bx+c���õ�����b��c�Ķ�Ԫһ�η����飬�ⷽ�������b��c��ֵ�����ݹ���ԭ��ԳƵĵ�������������C�����꣬���ô��뷨�����ж�C���ڴ��������ϣ�
��2�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=-x���ټ�����������ϴ��������ĵ�P��x��$\frac{1}{2}$x2-x-2����ʹ��������x�ᣬy��ĶԳƵ�M��Nǡ�ö���ֱ��BC�ϣ����ݺ���ͼ���ϵ�����������ó�����$\frac{1}{2}$x2-x-2=x���ⷽ�̼��������P�����ꣻ
��3�����ж��ı���PBQC��ƽ���ı��Σ�����ƽ���ı��ε����ʵó�����PBC������ʱ���ı���PBQC��������ֱ��BC����ƽ��t����λ�õ�ֱ��y=-x-t��������������ֻ��һ������ʱ����PBC�����������б�ʽ��=0���t��ֵ��������⼴�ɣ�
��� �⣺��1���߶��κ���y=$\frac{1}{2}$x2+bx+c��ͼ�����A��0��-2���͵�B��2��-2����
��$\left\{\begin{array}{l}{c=-2}\\{2+2b+c=-2}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-1}\\{c=-2}\end{array}\right.$��
��y=$\frac{1}{2}$x2-x-2��
�ߵ�C���B��������ԭ��Գƣ�
��C��-2��2����
��x=-2����y=$\frac{1}{2}$x2-x-2����y=$\frac{1}{2}$����-2��2-��-2��-2=2��
��C��-2��2���ڴ��������ϣ�
��2����ֱ��BC�Ľ���ʽΪy=mx+n��
��B��2��-2����C��-2��2����
��$\left\{\begin{array}{l}{2m+n=-2}\\{-2m+n=2}\end{array}\right.$�����$\left\{\begin{array}{l}{m=-1}\\{n=0}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=-x��
������������ϴ��������ĵ�P��x��$\frac{1}{2}$x2-x-2����ʹ��������x�ᣬy��ĶԳƵ�M��Nǡ�ö���ֱ��BC�ϣ�
��M��x��-$\frac{1}{2}$x2+x+2����N��-x��$\frac{1}{2}$x2-x-2����
��$\frac{1}{2}$x2-x-2=x��
���x=2��2$\sqrt{2}$��
�������P������Ϊ��2+2$\sqrt{2}$��2+2$\sqrt{2}$������2-2$\sqrt{2}$��2-2$\sqrt{2}$����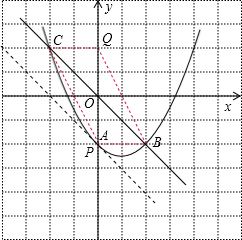 ��3���ߵ�C���B����ԭ��Գƣ���P���Q����ԭ��Գƣ�
��3���ߵ�C���B����ԭ��Գƣ���P���Q����ԭ��Գƣ�
���ı���PBQC��ƽ���ı��Σ�
��S?PBQC=2S��PBC��
�൱��PBC������ʱ���ı���PBQC��������
��ֱ��BC����ƽ��t����λ�õ�ֱ��y=-x-t��������������ֻ��һ������ʱ����PBC������
��y=-x-t����y=$\frac{1}{2}$x2-x-2����-x-t=$\frac{1}{2}$x2-x-2��
�����ã�$\frac{1}{2}$x2-2+t=0��
��=0-4��$\frac{1}{2}$��-2+t��=0��
���t=2��
�ⷽ��$\frac{1}{2}$x2-2+2=0�����x=0��
��y=-2����P��0��-2����
��ʱ�ı���PBQC����������ֵΪ��2��4=8��
���� �����Ƕ��κ������ۺ����ͣ������漰����֪ʶ�������ô���ϵ������һ�κ��������κ����Ľ���ʽ������ͼ���ϵ���������������������ᡢԭ��ԳƵĵ������������ƽ���ı��ε��ж������ʣ����κ�����һԪ���η��̵Ĺ�ϵ��֪ʶ���ۺ��Խ�ǿ���Ѷ����У��������ν���Լ�����˼���ǽ���Ĺؼ���

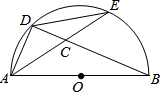 ��ͼ��ʾ��AB�ǡ�O��ֱ����D��E�ǰ�Բ���������㣬����AD��DE��AE��BD�ཻ�ڵ�C��Ҫ�ǡ�ADC���ABD���ƣ���������һ���������������ӵ������д�����ǣ�������
��ͼ��ʾ��AB�ǡ�O��ֱ����D��E�ǰ�Բ���������㣬����AD��DE��AE��BD�ཻ�ڵ�C��Ҫ�ǡ�ADC���ABD���ƣ���������һ���������������ӵ������д�����ǣ�������| A�� | ��ACD=��DAB | B�� | AD=DE | C�� | AD•AB=CD•BD | D�� | AD2=BD•CD |
| A�� | 12 | B�� | 14 | C�� | 16 | D�� | 17 |
| A�� | 0 | B�� | 1 | C�� | -1 | D�� | ��1 |

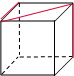 һ��ȫ�����������������һ����ɫ�Ľ���˿����ͼ������ô����˿������ͼ�е���״�ǣ�������
һ��ȫ�����������������һ����ɫ�Ľ���˿����ͼ������ô����˿������ͼ�е���״�ǣ�������