题目内容
18. 阅读理解:实数a>0,b>0,∵($\sqrt{a}$-$\sqrt{b}}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,即a+b≥2$\sqrt{ab}$.若ab=m(m为定值),则a+b≥2$\sqrt{m}$,当且仅当a=b时等式成立,即a=b时,a+b=2$\sqrt{m}$,∴当a=b=$\sqrt{m}$时,a+b取得最小值(填“最大”或“最小”).
阅读理解:实数a>0,b>0,∵($\sqrt{a}$-$\sqrt{b}}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,即a+b≥2$\sqrt{ab}$.若ab=m(m为定值),则a+b≥2$\sqrt{m}$,当且仅当a=b时等式成立,即a=b时,a+b=2$\sqrt{m}$,∴当a=b=$\sqrt{m}$时,a+b取得最小值(填“最大”或“最小”).理解应用:函数y=x+$\frac{2}{x}$(x>0),当x=$\sqrt{2}$时,y最小值=2$\sqrt{2}$.
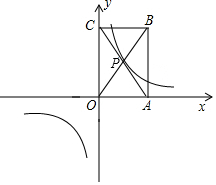
拓展应用:如图,双曲线y=$\frac{4}{x}$经过矩形OABC的对角线交点P,求矩形OABC的最小周长.
分析 (1)根据a+b≥2$\sqrt{m}$,当且仅当a=b时等式成立,即a=b时,a+b=2$\sqrt{m}$,进行判断即可;
(2)根据y=x+$\frac{2}{x}$(x>0),当x=$\frac{2}{x}$时,y有最小值,进行计算即可;
(3)先过P作PD⊥OA,设$P(x,\frac{4}{x})$,则$OD=x,PD=\frac{4}{x}$,根据${C_{矩形OABC}}=2(OA+AB)=4(x+\frac{4}{x})$,即可得到矩形OABC的最小周长.
解答  解:(1)∵a+b≥2$\sqrt{m}$,
解:(1)∵a+b≥2$\sqrt{m}$,
∴当a=b=$\sqrt{m}$时,a+b取得最小值,
故答案为:最小;
(2)∵y=x+$\frac{2}{x}$(x>0),
∴当x=$\frac{2}{x}$时,y有最小值,
即x=$\sqrt{2}$时,y最小值=$\sqrt{2}$+$\frac{2}{\sqrt{2}}$=2$\sqrt{2}$,
故答案为:$\sqrt{2},2\sqrt{2}$;
(3)如图所示,过P作PD⊥OA,
设$P(x,\frac{4}{x})$,则$OD=x,PD=\frac{4}{x}$,
∵四边形ABCO是矩形,
∴$OA=2x,AB=\frac{8}{x}$,
∴${C_{矩形OABC}}=2(OA+AB)=4(x+\frac{4}{x})$,
∵x>0且x•$\frac{4}{x}$=4为定值,
∴当x=$\frac{4}{x}$时,即x=2时,x+$\frac{4}{x}$有最小值4,
∴矩形OABC的最小周长为16.
点评 本题主要考查了反比例函数与一次函数交点问题,解决问题的关键是掌握完全平方公式的结构特征以及非负数的性质.

练习册系列答案
相关题目
13.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体x(kg)的关系如下表:
那么弹簧总长y(cm)与所挂物体质量x(kg)之间的函数关系式为y=6+0.5x.
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 |
3.下列说法正确的是( )
| A. | “任意一个三角形的外角和等于180°”这一事件是不可能事件 | |
| B. | 必然事件发生的概率为0 | |
| C. | 一组数据1,6,3,9,8的极差为7 | |
| D. | “面积相等的两个三角形全等”这一事件是必然事件 |
7.下列各数中,最小的数是( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | -$\sqrt{5}$ | D. | -3 |
8.下列图形中,∠2>∠1的是( )
| A. |  | B. |  平行四边形 | C. |  | D. |  |
 如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.