题目内容
2.关于x的不等式组$\left\{\begin{array}{l}{\frac{x+15}{2}>x-3}\\{\frac{2x+2}{3}<x+a}\end{array}\right.$有21个整数解,则a的取值范围是$\frac{2}{3}$<a≤1.分析 首先解不等式组确定不等式组的解集,然后根据不等式组有21个整数解即可得到关于a的不等式组,从而求解.
解答 解:$\left\{\begin{array}{l}{\frac{x+15}{2}>x-3…①}\\{\frac{2x+2}{3}<x+a…②}\end{array}\right.$,
解①得:x<21,
解②得:x>2-3a,
则不等式的解集是2-3a<x<21,
又∵不等式组有21个整数解,
∴-1≤2-3a<0,
解得:$\frac{2}{3}$<a≤1.
故答案是:$\frac{2}{3}$<a≤1.
点评 本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列事件中,是确定事件的是( )
| A. | 生病必须上医院 | |
| B. | 每年都是365天 | |
| C. | 3个人分成两组,一定有2个人分在一组 | |
| D. | 雨后有彩虹 |
7.方程2x=0的解是( )
| A. | x=-2 | B. | x=0 | C. | $x=-\frac{1}{2}$ | D. | $x=\frac{1}{2}$ |
 如图,点O是△ABC的∠ABC与∠ACB两个角的角平分线的交点,若∠BOC=118°,则∠A的角度是56°.
如图,点O是△ABC的∠ABC与∠ACB两个角的角平分线的交点,若∠BOC=118°,则∠A的角度是56°.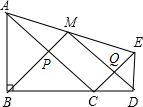 如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,给出下列结论:
如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,给出下列结论: