题目内容
5. 已知反比例函数y=$\frac{m-5}{x}$的图象的一支位于第二象限.
已知反比例函数y=$\frac{m-5}{x}$的图象的一支位于第二象限.(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
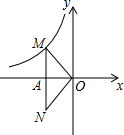
(2)如图,O为坐标原点,点M在该反比例函数位于第二象限的图象上,点N与点M关于x轴对称,若△OMN的面积为6,求m的值;
(3)在(2)的条件下,当2<MN<4时,求线段OA的取值范围(直接写出结果)
分析 (1)根据反比例函数的性质可得:双曲线的两支分别位于第一、第三象限时,m-5<0,再解即可;
(2)设M$({a,\frac{m-5}{a}})$,根据点N与点M关于x轴对称,可得N$({a,-\frac{m-5}{a}})$.然后表示出MN的长,再根据三角形的面积公式可得$\frac{1}{2}•({-a})•\frac{{2({m-5})}}{a}=6$,再解即可;
(3)首先计算出当MN=2时AO的值,再计算出当MN=4时AO的值,然后可得答案.
解答 解:(1)∵反比例函数$y=\frac{m-5}{x}$的图象的一支位于第二象限,
∴该函数图象的另一支位于第四象限.
∴m-5<0,解得m<5.
∴m的取值范围为m<5.
(2)设M$({a,\frac{m-5}{a}})$,
∵点N与点M关于x轴对称,
∴N$({a,-\frac{m-5}{a}})$.
∴MN=$\frac{m-5}{a}$-(-$\frac{m-5}{a}$)=$\frac{2(m-5)}{a}$,
OA=|a|=-a,
∴$\frac{1}{2}$×(-a)×$\frac{2(m-5)}{a}$=6,
解得:m=-1;
(3)当MN=2时,$\frac{1}{2}$×MN×AO=6,则AO=6,
当MN=4时,$\frac{1}{2}$×MN×AO=6,则AO=3,
∴当2<MN<4时,则3<OA<6.
点评 此题主要考查了反比例函数的性质,以及反比例函数图象上点的坐标特点,关键是掌握(1)反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.正确表示出M、N的坐标,MN的长.

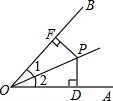 如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )| A. | PD=PF | B. | OD=OF | C. | ∠DPO=∠FPO | D. | PD=OD |
| A. | a3与a2 | B. | -3与a | C. | 2xy与2x | D. | $\frac{1}{2}{a^2}$与2a2 |
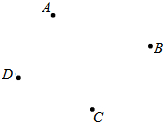 如图,已知四点A、B、C、D,请用尺规作图完成(保留作图痕迹)
如图,已知四点A、B、C、D,请用尺规作图完成(保留作图痕迹)