题目内容
10.已知一个圆内接正十二边形的面积为2,求这个圆的内接正六边形的面积.分析 设AB是正六边形的边,AC是正十二边形的边,则AB⊥OC,设圆的半径是r,根据△OAC的面积是正十二边形面积的$\frac{1}{12}$,即可列方程求得半径r的值,然后根据△OAB是等边三角形,求得△OAB的面积,进而求得正六边形的面积.
解答 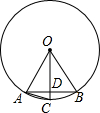 解:设AB是正六边形的边,AC是正十二边形的边,则AB⊥OC.
解:设AB是正六边形的边,AC是正十二边形的边,则AB⊥OC.
∵∠AOC=$\frac{360°}{12}$=30°,
∴设圆的半径是r,S△AOC=$\frac{1}{2}$OC•OA•sin30°=$\frac{1}{4}$r2=$\frac{2}{12}$,
∴r2=$\frac{2}{3}$.
∴S△OAB=$\frac{3\sqrt{3}}{4}$r2=$\frac{\sqrt{3}}{2}$.
则正六边形的面积是:6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$.
点评 本题考查学生对正多边形的概念掌握和计算的能力.解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
2. 如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )
如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )
 如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )
如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )| A. | 20° | B. | 100° | C. | 55° | D. | 40° |
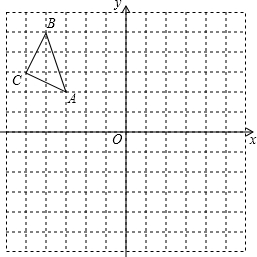 如图,在平面直角坐标系中,每个小正方形边长为1,点A的坐标为(-3,2),请按要求分别完成下列各小题:
如图,在平面直角坐标系中,每个小正方形边长为1,点A的坐标为(-3,2),请按要求分别完成下列各小题: 如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=35°,则∠AOD=110°.
如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=35°,则∠AOD=110°.
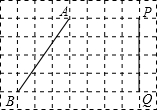 如图,方格纸中每个小正方形的边长均为1,线段AB和PQ的端点均在小正方形的顶点上.
如图,方格纸中每个小正方形的边长均为1,线段AB和PQ的端点均在小正方形的顶点上.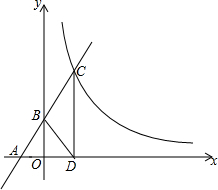 如图,在直角坐标系xOy中,一直线y=2x+b经过点A(-1,0)与y轴正半轴交于B点,在x轴正半轴上有一点D,且OB=OD,过D点作DC⊥x轴交直线y=2x+b于C点,反比例函数y=$\frac{k}{x}$(x>0)经过点C.
如图,在直角坐标系xOy中,一直线y=2x+b经过点A(-1,0)与y轴正半轴交于B点,在x轴正半轴上有一点D,且OB=OD,过D点作DC⊥x轴交直线y=2x+b于C点,反比例函数y=$\frac{k}{x}$(x>0)经过点C.