题目内容
15.(1)猜想与证明:如图(1),摆放着两个矩形纸片ABCD和矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的数量关系,并证明你的结论.
(2)拓展与延伸:
如图(2),若将”猜想与证明“中的矩形纸片换成正方形纸片ABCD和正方形纸片ECGF,并使点F在边CD上,点M仍为AF的中点,试猜想DM与ME的数量关系,并证明你的结论.
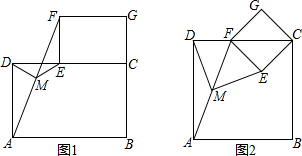
分析 (1)延长EM交AD于点H,由四边形ABCD和CEFG是矩形,根据矩形的性质得到对边平行,得到内错角相等,通过证明三角形全等,得到HM=EM,在RT△HDE中,HM=EM,得到DM=HM=ME,证出结果DM=ME;
(2)连接AC,由四边形ABCD和ECGF是正方形,得到∠FCE=45°,∠FCA=45°,证得AE和EC在同一条直线上,再由直角三角形的性质推出结论.
解答 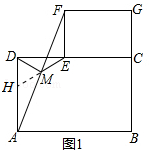 解:(1)猜想:DM=ME;
解:(1)猜想:DM=ME;
证明:如图1,延长EM交AD于点H,
∵四边形ABCD和CEFG是矩形,
∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,
$\left\{\begin{array}{l}∠EFM=∠HAM\\ FM=AM\\∠FME=∠AMH\end{array}\right.$,
∴△FME≌△AMH(ASA),
∴HM=EM,
在RT△HDE中,HM=EM,
∴DM=HM=ME,
∴DM=ME. 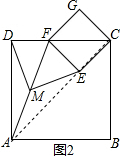
(2)猜想:DM=ME;
如图2,连接AC,
∵四边形ABCD和ECGF是正方形,
∴∠FCE=45°,∠FCA=45°,
∴AE和EC在同一条直线上,
在RT△ADF中,AM=MF,
∴DM=AM=MF,
在RT△AEF中,AM=MF,
∴AM=MF=ME,
∴DM=ME.
点评 本题考查了矩形的性质,全等三角形的判定与性质,直角三角形的性质,正方形的性质,正确的作出辅助线是本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
12.“从一个布袋中随机摸出1个球恰好是红球的概率为$\frac{1}{6}$”的意思是( )
| A. | 布袋中有1个红球和5个其它颜色的球 | |
| B. | 摸球6次就一定有1次摸中红球 | |
| C. | 如果摸球次数很多,那么平均每摸球6次就有1次摸中红球 | |
| D. | 布袋中共有6个红球,从中摸到了一个红球 |
9.若x>y,则下列式子错误的是( )
| A. | x-3>y-3 | B. | -3x>-3y | C. | 2x>y+x | D. | $\frac{x}{3}>\frac{y}{3}$ |
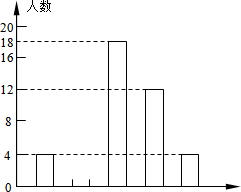 某校初三(1)班进行了一次跳绳测试,其中有8%的同学在17分以下,而且满分同学中只有1位男同学.体育委员将跳绳测试的统计结果绘制成如下的统计图,以便根据班级情况进行针对性训练.请你结合图中所给信息解答下列问题:
某校初三(1)班进行了一次跳绳测试,其中有8%的同学在17分以下,而且满分同学中只有1位男同学.体育委员将跳绳测试的统计结果绘制成如下的统计图,以便根据班级情况进行针对性训练.请你结合图中所给信息解答下列问题: