题目内容
18．
如图，点P是∠AOB内一点，分别作出P点关于OA、OB的对称点E、F，连接EF交OA于M，交OB于N，EF=15，求△PMN的周长．
分析 根据轴对称的性质可得PM=EM，PN=FN，然后求出△PMN的周长=EF．
解答 解：∵P点关于OA、OB的对称点分别为E、F，
∴PM=EM，PN=FN，
∴△PMN的周长=PM+MN+FN=ME+MN+FN=EF，
∵EF=15，
∴△PMN的周长=15．
点评 本题考查轴对称的性质，对应点的连线与对称轴的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
如图，在△ABC中，∠ABC=3∠C，AD平分∠BAC，BE⊥AD于E，求证：BE=$\frac{1}{2}$（AC-AB）．（提示：延长BE交AC于点F）．
3．
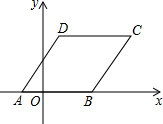如图坐标系，四边形ABCD是菱形，顶点A、B在x轴上，AB=5，点C在第一象限，且菱形ABCD的面积为20，A坐标为（-2，0），则顶点C的坐标为（ ）
如图坐标系，四边形ABCD是菱形，顶点A、B在x轴上，AB=5，点C在第一象限，且菱形ABCD的面积为20，A坐标为（-2，0），则顶点C的坐标为（ ）| A． | （4，3） | B． | （5，4） | C． | （6，4） | D． | （7，3） |
如图所示，平行四边形ABCD中，BC=2AB，AF=AB=BE，且点E，F在直线AB上，求∠EOF的度数．
一次函数与方程、不等式的关系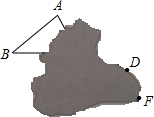
平移△ABC，使得边AB移到DE的位置，如图是小刚的作业，他的作法完全正确．可由于一不小心将一团墨汁沾染到了作业本上，请设法帮小刚补全平移前后的△ABC和△DEF．