题目内容
14.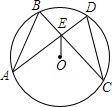 如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.(1)求证:BE=DE;
(2)如果⊙O的半径为5,AD⊥CB,DE=1,求AE的长.
分析 (1)根据圆心角、弧、弦的关系得到AB=CD,推出△ABE≌△CDE,根据全等三角形的性质得到结论;
(2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,根据垂径定理得到AF=FD,BG=OG,由于AD=BC,于是得到AF=CG,推出Rt△AOF≌Rt△OCG,根据全等三角形的性质得到OF=OG,证得四边形OFEG是正方形,于是得到OF=EF,设OF=EF=x,则AF=FD=x+1,根据勾股定理即可得到结论.
解答 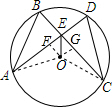 解:(1)∵$\widehat{AB}$=$\widehat{CD}$,
解:(1)∵$\widehat{AB}$=$\widehat{CD}$,
∴AB=CD,
在△ABE与△CDE中,$\left\{\begin{array}{l}{∠A=∠C}\\{AB=CD}\\{∠B=∠D}\end{array}\right.$,
∴△ABE≌△CDE,
∴BE=DE;
(2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,
根据垂径定理得:AF=FD,BG=OG,
∵AD=BC,
∴AF=OG,
在Rt△AOF与Rt△OCG中,$\left\{\begin{array}{l}{AF=CG}\\{OA=OC}\end{array}\right.$,
∴Rt△AOF≌Rt△OCG,
∴OF=OG,
∵AD⊥CB,
∴四边形OFEG是正方形,
∴OF=EF,
设OF=EF=x,
则AF=FD=x+1,
∴OF2+AF2=OA2,
即:x2+(x+1)2=52,
解得:x=3,x=-4(舍去),
∴AF=4,
∴AE=7.
点评 本题考查了全等三角形的判定和性质,圆心角、弧、弦的关系,勾股定理,熟练则全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
4. 如图,已知∠B=∠C,则( )
如图,已知∠B=∠C,则( )
 如图,已知∠B=∠C,则( )
如图,已知∠B=∠C,则( )| A. | ∠1>∠2 | B. | ∠1=∠2 | ||
| C. | ∠1<∠2 | D. | 无法确定∠1和∠2的大小关系 |
5.下列计算正确的是( )
| A. | 23=2×3 | B. | -210=(-2)10 | C. | (-2)3=-23 | D. | (2+3)2=22+32 |
2. 小手盖住的点的坐标可能为( )
小手盖住的点的坐标可能为( )
 小手盖住的点的坐标可能为( )
小手盖住的点的坐标可能为( )| A. | (3,-4) | B. | (-6,3) | C. | (5,2) | D. | (-4,-6) |
3.三角形的下列线段中,能将三角形的面积分成相等两部分的一定是( )
| A. | 中线 | B. | 角平分线 | ||
| C. | 高 | D. | 一边的垂直平分线 |
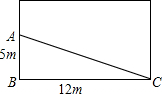 如图,长方形的花圃中,有人避开拐角线A→B→C而直接走“捷径”AC,小明想在A处树立一个标牌“少走4米,踏之何忍”,请根据图中数字计算完成标牌中未填的数字.
如图,长方形的花圃中,有人避开拐角线A→B→C而直接走“捷径”AC,小明想在A处树立一个标牌“少走4米,踏之何忍”,请根据图中数字计算完成标牌中未填的数字. 如图,四边形ABCD中,∠A=∠BDC=90°,AD=3,AB=4,CD=12,求BC的长.
如图,四边形ABCD中,∠A=∠BDC=90°,AD=3,AB=4,CD=12,求BC的长.