题目内容
4. 如图,四边形ABCD中,∠A=∠BDC=90°,AD=3,AB=4,CD=12,求BC的长.
如图,四边形ABCD中,∠A=∠BDC=90°,AD=3,AB=4,CD=12,求BC的长.
分析 连接BD,首先由勾股定理求出BD,再由勾股定理求出BC的长即可.
解答  解:连接BD,如图所示:
解:连接BD,如图所示:
∵∠A=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵∠BDC=90°,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13.
点评 本题考查了勾股定理;熟练掌握勾股定理,由勾股定理求出BD是解决问题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
14.已知xy=2,x+y=3,则x-y的值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 不能确定 |
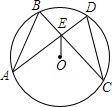 如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.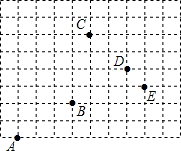 如图,用(1,0)表示A点的位置,那么:
如图,用(1,0)表示A点的位置,那么: