题目内容
9.观察下列一组等式的化简.然后解答后面的 问题:$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}-1$;$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}-\sqrt{2}$;
$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{1×(\sqrt{4}-\sqrt{3})}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=2-$\sqrt{3}$…
(1)在计算结果中找出规律$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$(n表示大于0的自然数)
(2)通过上述化简过程,可知$\sqrt{11}-\sqrt{10}$>$\sqrt{12}-\sqrt{11}$(天“>”、“<”或“=”);
(3)利用你发现的规律计算下列式子的值:
($\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}+$…+$\frac{1}{\sqrt{2016}+\sqrt{2015}}$)($\sqrt{2016}+1$)
分析 (1)根据平方差公式,可得答案;
(2)根据分母有理化,可得答案;
(3)根据分母有理化,可得平方差公式,根据平方差公式,可得答案.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;
(2)$\sqrt{11}$-$\sqrt{10}$=$\frac{1}{\sqrt{11}+\sqrt{10}}$,$\sqrt{12}$-$\sqrt{11}$=$\frac{1}{\sqrt{12}+\sqrt{11}}$,
$\sqrt{11}$-$\sqrt{10}$>$\sqrt{12}$-$\sqrt{11}$;
(3)原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2016}$-$\sqrt{2015}$)($\sqrt{2016}$+1)
=($\sqrt{2016}$-1)($\sqrt{2016}$+1)
=2016-1
=2015.
点评 本题考查了分母有理化,利用平方差公式是分母有理化的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.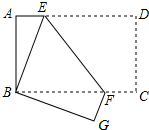 如图,将长方形纸片ABCD折叠,使点D与B重合,点C落到G处,折痕为EF,若∠ABE=20°,则∠EFG的度数为( )
如图,将长方形纸片ABCD折叠,使点D与B重合,点C落到G处,折痕为EF,若∠ABE=20°,则∠EFG的度数为( )
 如图,将长方形纸片ABCD折叠,使点D与B重合,点C落到G处,折痕为EF,若∠ABE=20°,则∠EFG的度数为( )
如图,将长方形纸片ABCD折叠,使点D与B重合,点C落到G处,折痕为EF,若∠ABE=20°,则∠EFG的度数为( )| A. | 125° | B. | 120° | C. | 135° | D. | 150° |
4. 如图所示,一只蚂蚁在正方体的一个顶点A处,它能爬到顶点B处寻找食物,若这个正方体的边长为1,则这只蚂蚁所爬行的最短路程为( )
如图所示,一只蚂蚁在正方体的一个顶点A处,它能爬到顶点B处寻找食物,若这个正方体的边长为1,则这只蚂蚁所爬行的最短路程为( )
 如图所示,一只蚂蚁在正方体的一个顶点A处,它能爬到顶点B处寻找食物,若这个正方体的边长为1,则这只蚂蚁所爬行的最短路程为( )
如图所示,一只蚂蚁在正方体的一个顶点A处,它能爬到顶点B处寻找食物,若这个正方体的边长为1,则这只蚂蚁所爬行的最短路程为( )| A. | 8 | B. | $\sqrt{2}+1$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
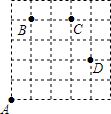 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A→B(+1,+4),从D到C记为:D→C(-1,+2),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A→B(+1,+4),从D到C记为:D→C(-1,+2),其中第一个数表示左右方向,第二个数表示上下方向.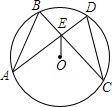 如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.