题目内容
11.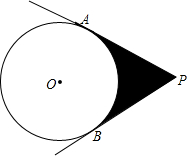 如图,PA,PB是⊙O的两条切线,切点分别为A,B,⊙O的半径为2cm,∠P=60°,求图中阴影部分的面积.
如图,PA,PB是⊙O的两条切线,切点分别为A,B,⊙O的半径为2cm,∠P=60°,求图中阴影部分的面积.
分析 连接OA、OB,OP,如图,根据切线的性质和切线长定理得到∠PAO=∠PBO=90°,∠APO=30°,则根据四边形内角和得到∠AOB=180°-∠APB=120°,再在Rt△PAO中利用含30度的直角三角形三边的关系得到AP=$\sqrt{3}$OA=2$\sqrt{3}$,则S△PAO=2$\sqrt{3}$,然后根据扇形面积公式,利用阴影部分的面积=S四边形AOBP-S扇形AOB进行计算.
解答 解:连接OA、OB,OP,如图,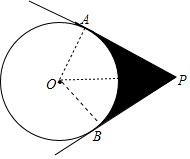
∵PA,PB是⊙O的两条切线,
∴OA⊥AP,OB⊥PB,OP平分∠APB,
∴∠PAO=∠PBO=90°,∠APO=$\frac{1}{2}$×60°=30°,
∴∠AOB=180°-∠APB=180°-60°=120°,
在Rt△PAO中,∵OA=2,∠APO=30°,
∴AP=$\sqrt{3}$OA=2$\sqrt{3}$,
∴S△PAO=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
∴阴影部分的面积=S四边形AOBP-S扇形AOB
=2×2$\sqrt{3}$-$\frac{120•π•{2}^{2}}{360}$
=4$\sqrt{3}$-$\frac{4}{3}$π.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.会利用面积的和差计算不规则图形的面积.

练习册系列答案
相关题目
1.下列说法:
①-$\sqrt{17}$是17的平方根;
②$\frac{1}{27}$的立方根是±$\frac{1}{3}$;
③-81没有立方根;
④互为相反数的两个数的立方根也互为相反数,
错误的有( )
①-$\sqrt{17}$是17的平方根;
②$\frac{1}{27}$的立方根是±$\frac{1}{3}$;
③-81没有立方根;
④互为相反数的两个数的立方根也互为相反数,
错误的有( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
6.圆柱的侧面展开图( )
| A. | 是平行四边形 | B. | 一定是正方形 | C. | 可能是菱形 | D. | 必是矩形 |
 ,则该车牌照上的数字为550.
,则该车牌照上的数字为550.