题目内容
15．下列性质中正方形具有而矩形不具有的是（ ）| A． | 对边相等 | B． | 对角线相等 | C． | 四个角都是直角 | D． | 对角线互相垂直 |
分析 根据矩形是特殊的正方形，因而矩形具有的性质一定是正方形具有的性质，据此即可作出判断．
解答 解：A、B、C都是矩形的性质，正方形是特殊的矩形，矩形的性质一定是正方形的性质，因而A、B、C错误；
正方形的对角线互相垂直，但矩形的对角线不一定互相垂直，故D正确．
故选D．
点评 本题主要考查了正方形与矩形的性质，正确记忆两个图形的性质，理解两者之间的关系是关键．
练习册系列答案
名校课堂系列答案
相关题目
3．在平面直角坐标系中，点（1，-2）关于x轴的对称点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
10．下列计算正确的是（ ）
| A． | $\sqrt{27}$$÷\sqrt{3}$=3 | B． | 3+$\sqrt{3}$=3$\sqrt{3}$ | C． | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ | D． | $\sqrt{（-2）^{2}}$=-2 |
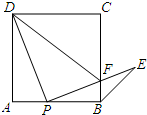如图，点P是正方形ABCD边AB上一点（点P不与点A，B重合），连接PD，将线段PD绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F，连接BE，DF．
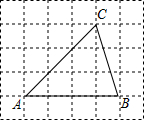如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．