题目内容
1．如果⊙O1与⊙O2的圆心都在x轴上，⊙O1的圆心坐标为（7，0），半径为1，⊙O2的圆心坐标为（m，0），半径为2，则当2＜m＜4时，两圆的位置关系是（ ）| A． | 相交 | B． | 相切 | C． | 相离 | D． | 内含 |
分析 先根据m的取值范围求得d的取值范围，然后根据d、r、R之间的关系求解即可．
解答 解：∵d=7-m，2＜m＜4，
∴5＜d＜3．
又∵r=1，R=2，
∴d＞r+R．
故选：C．
点评 本题主要考查的是圆和圆的位置关系，求得d的取值范围是解题的关键．
练习册系列答案
相关题目
12．
已知二次函数y=x2-4x+3．
（1）求出该函数与x轴的交点坐标、与y轴的交点坐标；
（2）在平面直角坐标系中，用描点法画出该二次函数的图象；
（3）根据图象回答：
①当自变量x的取值范围满足什么条件时，y＜0？
②当0≤x＜3时，y的取值范围是多少？
已知二次函数y=x2-4x+3．（1）求出该函数与x轴的交点坐标、与y轴的交点坐标；
（2）在平面直角坐标系中，用描点法画出该二次函数的图象；
| x | … | … | |||||
| y | … | … |
①当自变量x的取值范围满足什么条件时，y＜0？
②当0≤x＜3时，y的取值范围是多少？
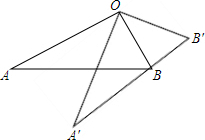如图，∠AOB=90°，将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′，使点B恰好落在边A′B′上．已知tanB=2，OB=5，则BB′=2$\sqrt{5}$．
16．已知点（-2，y1），（3，y2）都在直线y=-x+b上，则y1与y2的大小关系是（ ）
| A． | y1＜y2 | B． | y1=y2 | C． | y1＞y2 | D． | 无法确定 |
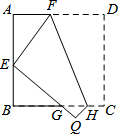如图，已知正方形ABCD边长为6，将其折叠，使点D落在AB边的中点E处，折痕为FH，点C落在Q处，EQ与BC交于点G，则△EBG的周长是（ ）
如图所示的图形绕虚线旋转一周得到的几何体的名称是圆锥．