题目内容
3.计算(1)$\frac{\sqrt{12}×\sqrt{6}}{\sqrt{24}}$
(2)$\sqrt{12}$-$\sqrt{3}$-$\sqrt{\frac{1}{3}}$
(3)(2-$\sqrt{10}$)2+$\sqrt{40}$
(4)($\sqrt{11}$-$\sqrt{7}$)($\sqrt{11}$+$\sqrt{7}$)-$\sqrt{25}$
(5)|$\sqrt{3}$-2|+(2016-π)0-(-$\frac{1}{3}$)-2+3×$\frac{1}{\sqrt{3}}$.
分析 (1)利用二次根式的乘除法则运算;
(2)先把二次根式化为最简二次根式,然后合并即可;
(3)利用完全平方公式计算;
(4)利用平方差公式计算;
(5)根据零指数幂和负整数指数幂的意义计算.
解答 解:(1)原式=$\sqrt{\frac{12×6}{24}}$
=$\sqrt{3}$;
(2)原式=2$\sqrt{3}$-$\sqrt{3}$-$\frac{\sqrt{3}}{3}$
=$\frac{2\sqrt{3}}{3}$;
(3)原式=4-4$\sqrt{10}$+10+2$\sqrt{10}$
=14-2$\sqrt{10}$;
(4)原式=11-7-5
=-1;
(5)原式=2-$\sqrt{3}$+1-9+$\sqrt{3}$
=-6.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
11. 如图,直线AB、CD相交于E,EF平分∠BED,已知∠DEF=70°,则∠AED的度数是( )
如图,直线AB、CD相交于E,EF平分∠BED,已知∠DEF=70°,则∠AED的度数是( )
 如图,直线AB、CD相交于E,EF平分∠BED,已知∠DEF=70°,则∠AED的度数是( )
如图,直线AB、CD相交于E,EF平分∠BED,已知∠DEF=70°,则∠AED的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
12.比较2100与375的大小:因为2100=(24)25=1625,375=(33)25=2725,而16<27,所以1625<2725,即2100<375.据此可知355、444、533的大小关系是( )
| A. | 355<444<533 | B. | 533<444<355 | C. | 444<533<355 | D. | 533<355<444 |
13.当x取何值时,代数式x2-6x-3的值最小( )
| A. | 0 | B. | -3 | C. | 3 | D. | -9 |
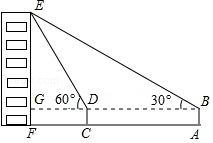 如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据$\sqrt{3}$=1.732)
如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据$\sqrt{3}$=1.732) 如图所示,直线a、b被c、d所截,且c⊥a,c⊥b,∠1=70°,求∠3的大小?
如图所示,直线a、b被c、d所截,且c⊥a,c⊥b,∠1=70°,求∠3的大小?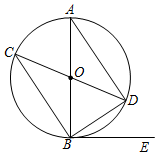 已知如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
已知如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.