Question

8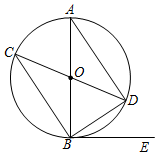．已知如图，在⊙O中，AB，CD是直径，BE是切线，B为切点，连接AD，BC，BD．
（1）求证：△ABD≌△CDB；
（2）若∠DBE=35°，求∠ADC的度数．

Answer 1

分析 （1）先根据直径的性质得：∠ADB=∠CBD=90°，AB=CD，利用AAS证明△ABD≌△CDB；
（2）根据切线的性质得：∠ABE=90°，求出∠ABD=55°，再由直径所对的圆周角为直角和同弧所对的圆周角相等得：∠ADC=∠CBA=35°．

解答 证明：（1）∵在⊙O中，AB，CD是直径，
∴∠ADB=∠CBD=90°，
AB=CD，
在△ABD和△CDB中，
∵$\left\{\begin{array}{l}{∠C=∠A}\\{∠CBD=∠ADB}\\{CD=AB}\end{array}\right.$，
∴△ABD≌△CDB（AAS）；
（2）∵BE是切线，B为切点，AB是直径，
∴∠ABE=90°，
∵∠DBE=35°，
∴∠ABD=55°，
∵∠CBD=90°，
∴∠CBA=35°，
∴∠ADC=∠CBA=35°．

点评 本题考查了切线的性质、全等三角形的性质和判定、圆周角定理，难度不大，熟练掌握直径所对的圆周角是直角是关键．