题目内容
18.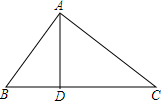 已知:如图,在△ABC中,AD⊥BC,垂足为D,且BC=16,AB=DC,cos∠ABC=$\frac{3}{5}$.(1)求:BD的长;(2)求:tanC的值.
已知:如图,在△ABC中,AD⊥BC,垂足为D,且BC=16,AB=DC,cos∠ABC=$\frac{3}{5}$.(1)求:BD的长;(2)求:tanC的值.
分析 (1)由cos∠ABC=$\frac{3}{5}$,设BD=3k.AB=5k,根据AB=DC,得到CD=5k,然后由BC=BD+CD=8k=16,即可得到结果;
(2)又BD=6,得到CD=AB=10,根据勾股定理得到AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=8,即可得到结论.
解答 解:(1)∵cos∠ABC=$\frac{3}{5}$,
设BD=3k.AB=5k,
∵AB=DC,
∴CD=5k,
∴BC=BD+CD=8k=16,
∴k=2,
∴BD=6;
(2)∵BD=6,
∴CD=AB=10,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=8,
∴tanC=$\frac{AD}{CD}$=$\frac{8}{10}$=$\frac{4}{5}$.
点评 本题考查了解直角三角形,熟练掌握解直角三角形的方法是解题的关键.

练习册系列答案
相关题目
7.在平面直角坐标系中,设点A(-8,3)、B(-4,5)及动点C(0,n),D (m,0),当四边形ABCD的周长最小时,C、D的位置的确定方法正确的是( )
| A. | 作点A关于x轴的对称点A′,点B关于y轴的对称点B′,连接A′B′交x轴于点D,交y轴于C | |
| B. | 作点A关于x轴的对称点A′,点B关于y轴的对称点B′,连接A′B′交x轴于点C,交y轴于D | |
| C. | 过A作AD⊥x轴于D点,过B作BC⊥y轴于C点 | |
| D. | 过A作AC⊥x轴于C点,过B作BD⊥y轴于D点 |
 直线m的图象如图所示.试求y与x的函数关系式.小华的解法为:设y=kx.由图象可得2=3k.故k=$\frac{2}{3}$.所以y与x的函数关系式为y=$\frac{2}{3}$x,请你评判小华的做法,如果不正确.请给出正确的作法.
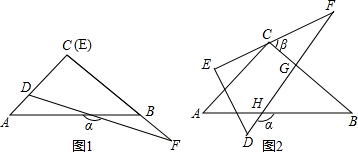
直线m的图象如图所示.试求y与x的函数关系式.小华的解法为:设y=kx.由图象可得2=3k.故k=$\frac{2}{3}$.所以y与x的函数关系式为y=$\frac{2}{3}$x,请你评判小华的做法,如果不正确.请给出正确的作法. 如图,AB为⊙O直径,BF⊥AB,E为BF上一点,AE和AF交⊙O于C和D,求证:C、D、F、E四点共圆.
如图,AB为⊙O直径,BF⊥AB,E为BF上一点,AE和AF交⊙O于C和D,求证:C、D、F、E四点共圆.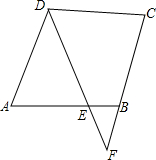 如图,在?ABCD中,AD=4,AE:CD=2:3,DE与CB的延长线交于点F,求CF的长.
如图,在?ABCD中,AD=4,AE:CD=2:3,DE与CB的延长线交于点F,求CF的长.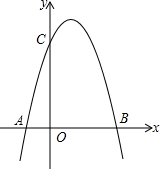 如图,二次函数的图象经过A、B、C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC.
如图,二次函数的图象经过A、B、C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC.