题目内容
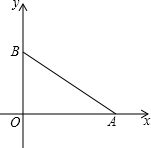 如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位.
如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位.(1)当t=1秒时,求△OPQ的面积;
(2)在前3秒内,求△OPQ的最大面积.
考点:一次函数的应用,解一元二次方程-配方法,三角形的面积
专题:
分析:(1)由于A(8,0),B(0,6),得出OB=6,OA=8,AB=10.当t=1秒时,点P在OB上,点Q在OA上,设经过t秒,利用△OPQ的面积=
OP•OQ求出即可;
(2)同理,根据在前3秒内,点P在OB上,点Q在OA上,设经过t秒,利用△OPQ的面积=
OP•OQ求出最值即可.
| 1 |
| 2 |
(2)同理,根据在前3秒内,点P在OB上,点Q在OA上,设经过t秒,利用△OPQ的面积=
| 1 |
| 2 |
解答:解:(1)∵A(8,0),B(0,6),
∴OB=6,OA=8,AB=10
∴当t=1s时,BP=2,OP=4,OQ=1
∴△OPQ的面积=
•1•4=2;
(2)在前3秒内,点P在OB 上,点Q 在OA 上,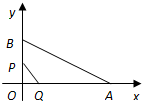
设经过t秒,点P,Q位置如图.
则OP=6-2t,OQ=t.
△OPQ的面积=
OP•OQ=t(3-t),
当t=
时,Smax=
.
∴OB=6,OA=8,AB=10
∴当t=1s时,BP=2,OP=4,OQ=1
∴△OPQ的面积=
| 1 |
| 2 |
(2)在前3秒内,点P在OB 上,点Q 在OA 上,

设经过t秒,点P,Q位置如图.
则OP=6-2t,OQ=t.
△OPQ的面积=
| 1 |
| 2 |
当t=
| 3 |
| 2 |
| 9 |
| 4 |
点评:此题主要考查了一次函数的应用以及三角形的面积,把动点问题与实际相结合,此题难度不大,解答此题的关键是需要结合相应的图形解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
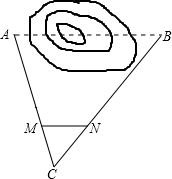 如图,A、B两点被池塘隔开,在AB外任取一点C,连结AC、BC分别取其三等分点M,N(M、N两点均靠近点C).量得MN=27m,则AB的长是( )
如图,A、B两点被池塘隔开,在AB外任取一点C,连结AC、BC分别取其三等分点M,N(M、N两点均靠近点C).量得MN=27m,则AB的长是( )| A、54m | B、81m |
| C、108m | D、135m |
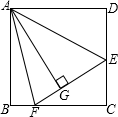 在正方形ABCD中,E、F分别是BC、CD上的点,∠EAF=45°,AG⊥EF,垂足为G,求证:AB=AG.
在正方形ABCD中,E、F分别是BC、CD上的点,∠EAF=45°,AG⊥EF,垂足为G,求证:AB=AG.