题目内容
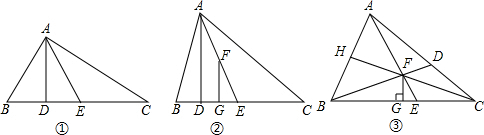
如图①所示△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=70°,∠C=30°,求∠DAE的度数;
(2)若△ABC中,∠B=α,∠C=β(α>β),请你根据第一问的结果大胆猜想∠DAE与α、β间的等量关系,不必说明理由;
(3)如图②,在△ABC中,AD⊥BC,AE平分∠BAC,F是AE上的任意一点,过F作FG⊥BC于G,且∠B=80°,∠C=30°,请你直接运用(2)中结论求出∠EFG的度数;
(4)在(3)的条件下,若F点在AE的延长线上,其他条件不变,则∠EFG的大小发生改变吗?请说明理由;
(5)如图③,在△ABC中,点F是三角形的三条角平分线的交点,∠ABC=60°,∠ACB=20°,且FG⊥BC于G,试求∠FEG的度数.
(1)若∠B=70°,∠C=30°,求∠DAE的度数;
(2)若△ABC中,∠B=α,∠C=β(α>β),请你根据第一问的结果大胆猜想∠DAE与α、β间的等量关系,不必说明理由;
(3)如图②,在△ABC中,AD⊥BC,AE平分∠BAC,F是AE上的任意一点,过F作FG⊥BC于G,且∠B=80°,∠C=30°,请你直接运用(2)中结论求出∠EFG的度数;
(4)在(3)的条件下,若F点在AE的延长线上,其他条件不变,则∠EFG的大小发生改变吗?请说明理由;
(5)如图③,在△ABC中,点F是三角形的三条角平分线的交点,∠ABC=60°,∠ACB=20°,且FG⊥BC于G,试求∠FEG的度数.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据直角三角形两锐角互余求出∠BAD,再根据三角形的内角和定理求出∠BAC,根据角平分线的定义求出∠BAE,然后根据∠DAE=∠BAE-∠BAD代入数据计算即可得解;
(2)把∠B、∠C的度数换成α、β解答即可;
(3)求出∠DAE,再根据两直线平行,同位角相等可得∠EFG=∠DAE;
(4)两直线平行,内错角相等可得∠EFG=∠DAE;
(5)根据三角形的内角和定理求出∠BAC,再根据角平分线的定义求出∠CAE,然后根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FEG=∠CAE+∠ACB代入数据计算即可得解.
(2)把∠B、∠C的度数换成α、β解答即可;
(3)求出∠DAE,再根据两直线平行,同位角相等可得∠EFG=∠DAE;
(4)两直线平行,内错角相等可得∠EFG=∠DAE;
(5)根据三角形的内角和定理求出∠BAC,再根据角平分线的定义求出∠CAE,然后根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FEG=∠CAE+∠ACB代入数据计算即可得解.
解答:解:(1)∵AD⊥BC,
∴∠BAD=90°-∠B=90°-70°=20°,
∵∠B=70°,∠C=30°,
∴∠BAC=180°-70°-30°=80°,
∵AE平分∠BAC,
∴∠BAE=
∠BAC=
×80°=40°,
∴∠DAE=∠BAE-∠BAD=40°-20°=20°;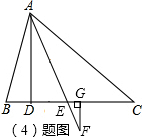
(2)∠DAE=
(180°-α-β)-(90°-α)=
(α-β),
故,∠DAE=
(α-β);
(3)∠DAE=
(80°-30°)=25°;
(4)如图,F点在AE的延长线上时,
∵AD⊥BC,EF⊥BC,
∴AD∥GF,
∴∠EFG=∠DAE=
(α-β),大小不发生变化;
(5)∵∠ABC=60°,∠ACB=20°,
∴∠BAC=180°-60°-20°=100°,
∵AE是∠BAC的平分线,
∴∠CAE=
∠BAC=
×100°=50°,
∴∠FEG=∠CAE+∠ACB=50°+20°=70°.
∴∠BAD=90°-∠B=90°-70°=20°,
∵∠B=70°,∠C=30°,
∴∠BAC=180°-70°-30°=80°,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DAE=∠BAE-∠BAD=40°-20°=20°;

(2)∠DAE=
| 1 |
| 2 |
| 1 |
| 2 |
故,∠DAE=
| 1 |
| 2 |
(3)∠DAE=
| 1 |
| 2 |
(4)如图,F点在AE的延长线上时,
∵AD⊥BC,EF⊥BC,
∴AD∥GF,
∴∠EFG=∠DAE=
| 1 |
| 2 |
(5)∵∠ABC=60°,∠ACB=20°,
∴∠BAC=180°-60°-20°=100°,
∵AE是∠BAC的平分线,
∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FEG=∠CAE+∠ACB=50°+20°=70°.
点评:本题考查了三角形的内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,平行线的性质,熟记各性质并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
下列各数中:+3、3、-
、9、
、-(-8)、0、-|+3|,负有理数有( )
| 2 |
| 3 |
| 7 |
| 5 |
| A、2个 | B、3个 | C、4个 | D、5个 |
用一个平面去截圆柱体,则截面形状不可能是( )
| A、梯形 | B、正方形 | C、长方形 | D、圆 |
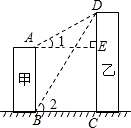 如图,线段AB、DC分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,从A点测得D点的仰角∠1为30°,从B点测得D点的仰角∠2为60°,已知乙建筑物的高CD=36米.
如图,线段AB、DC分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,从A点测得D点的仰角∠1为30°,从B点测得D点的仰角∠2为60°,已知乙建筑物的高CD=36米.