题目内容
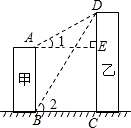如图，线段AB、DC分别表示甲、乙两建筑物的高，AB⊥BC，DC⊥BC，从A点测得D点的仰角∠1为30°，从B点测得D点的仰角∠2为60°，已知乙建筑物的高CD=36米．（1）求甲、乙两建筑物之间的距离BC；
（2）求甲建筑物的高AB．
考点：解直角三角形的应用-仰角俯角问题
专题：
分析：（1）首先分析图形，根据题意构造直角三角形，在直角三角形△ADE中，DE的长度为x，再表示出AE，在直角三角形△BCD中，利用三角函数求出BC的长；
（2）借助AE=BC继而可求得甲建筑物的高度．
（2）借助AE=BC继而可求得甲建筑物的高度．
解答：解：（1）根据题意，得∠DBC=∠2=60°，∠DAE=∠1=30°，AE=BC，EC=AB．
设DE=x，则AB=EC=CD-DE=36-x，
在Rt△AED中，tan∠DAE=tan30°=
，
∴AE=
=
=
x，
∴BC=AE=
x．
在Rt△DCB中，tan∠DBC=tan60°=
，
∴
=
，
∴3x=36，
x=12，
经检验x=12是原方程的解．
∴AE=BC=12
，
∴甲、乙两建筑物之间的距离BC为12
米；
（2）∵BC=AE=12
，x=12，
∴EC=36-x=36-12=24（米）．
答：甲建筑物之间的高AB为24米．
设DE=x，则AB=EC=CD-DE=36-x，
在Rt△AED中，tan∠DAE=tan30°=
| DE |
| AE |
∴AE=
| DE |
| tan30° |
| x | ||||
|
| 3 |
∴BC=AE=
| 3 |
在Rt△DCB中，tan∠DBC=tan60°=
| DC |
| BC |
∴
| 3 |
| 36 | ||
|
∴3x=36，
x=12，
经检验x=12是原方程的解．
∴AE=BC=12
| 3 |
∴甲、乙两建筑物之间的距离BC为12
| 3 |
（2）∵BC=AE=12
| 3 |
∴EC=36-x=36-12=24（米）．
答：甲建筑物之间的高AB为24米．
点评：本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
下列各题中计算结果正确的是（ ）
| A、2x+3y=5xy | ||
B、3.5ba-
| ||
| C、4a2b-5ab2=-ab | ||
| D、x2+x=x3 |
如图所示，A、M、N点坐标分别为A（0，1），M（3，2），N（4，4），动点P从点A出发，沿y轴以每秒一个单位长度的速度向上移动，且过点P的直线l：y=-x+b也随之移动，设移动时间为t秒．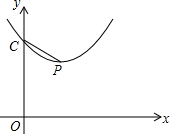
如图，已知抛物线y=ax2+bx+c的顶点为P，抛物线交y轴于C点．