题目内容
有一个运算程序,可以使得:a⊕b=n,则(a+1)⊕b=n+1,a⊕(b+1)=n-2,现在已知1⊕1=2,则2014⊕2014= .
考点:规律型:数字的变化类
专题:新定义
分析:利用归纳法解答,根据题目给出的例子,求得2⊕1=2+1=3,2⊕2=3-2=1,3⊕2=1+1=2,3⊕3=2-2=0,同样的我们可以求得4⊕4=-1,5⊕5=-2…,2014⊕2014=-2011.规律为:前项增一,结果加一,后项增一,结果减二.
解答:解:规律为前一项增一,结果加一,后一项增一,结果减二,
则1⊕1=2,2014⊕2014为2加上2013个1减去2013个2,
即2014⊕2014=2+2013×1-2013×2=-2011.
故答案为:-2011.
则1⊕1=2,2014⊕2014为2加上2013个1减去2013个2,
即2014⊕2014=2+2013×1-2013×2=-2011.
故答案为:-2011.
点评:此题主要考查了数字变化规律,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律,关键是分析得到⊕的运算规律.

练习册系列答案
相关题目
下列函数:xy=1,y=
,y=
,y=
,y=2x2中,是y关于x的反比例函数的有( )个.
| x |
| 3 |
| k |
| y |
| 1 |
| x-2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
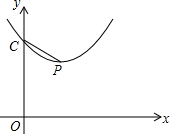 如图,已知抛物线y=ax2+bx+c的顶点为P,抛物线交y轴于C点.
如图,已知抛物线y=ax2+bx+c的顶点为P,抛物线交y轴于C点.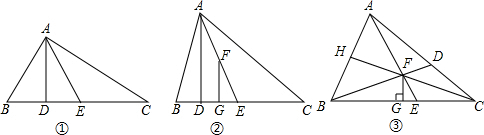
 如图,点A、B在圆O上,△OAB是等边三角形,延长OA到C,使得AC=OA,连接BC.在圆O上是否存在一点D,使得BD=BC?
如图,点A、B在圆O上,△OAB是等边三角形,延长OA到C,使得AC=OA,连接BC.在圆O上是否存在一点D,使得BD=BC?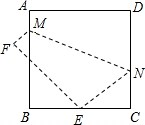 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.