题目内容
已知两圆的圆心距是9，两圆的半径是方程x2-12x+35=0的两根，则两圆有 条切线．
考点：圆与圆的位置关系,解一元二次方程-因式分解法
专题：
分析：由两圆的圆心距是9，两圆的半径是方程x2-12x+35=0的两根，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系得出两圆位置关系，继而求得答案．
解答：解：∵两圆的半径是方程x2-12x+35=0的两根，
∴（x-5）（x-7）=0，
解得：x1=5，x2=7，
∴两圆的半径分别为：5，7；
∴两圆的半径和为12，半径差为2，
∵两圆的圆心距是9，
∴此两圆相交，
∴两圆有2条切线．
故答案为：2．
∴（x-5）（x-7）=0，
解得：x1=5，x2=7，
∴两圆的半径分别为：5，7；
∴两圆的半径和为12，半径差为2，
∵两圆的圆心距是9，
∴此两圆相交，
∴两圆有2条切线．
故答案为：2．
点评：此题考查了圆与圆的位置关系．此题比较简单，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系是解此题的关键．
练习册系列答案
相关题目
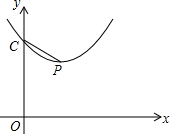如图，已知抛物线y=ax2+bx+c的顶点为P，抛物线交y轴于C点．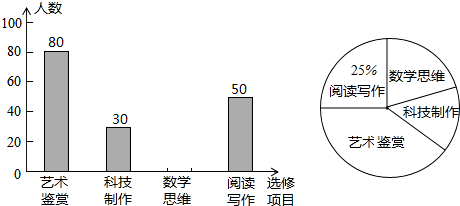
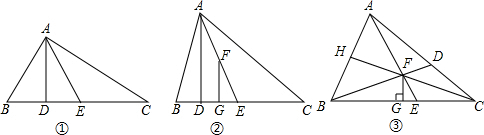
如图，点A、B在圆O上，△OAB是等边三角形，延长OA到C，使得AC=OA，连接BC．在圆O上是否存在一点D，使得BD=BC？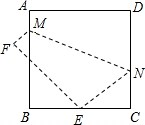
如图，将边长为8cm的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN．