Question

19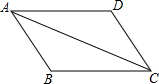．如图，AB∥CD，∠B=∠D，则线段AD、BC有何关系？请说明理由．

Answer 1

分析 证明△ABC≌△CDA，然后根据全等三角形的对应边相等，对应角相等，以及平行线的判定定理即可解答．

解答 解：AD∥BC，且AD=BC．
理由是：∵AB∥CD，
∴∠BAC=∠DCA．
∴在△ABC和△CDA中，
$\left\{\begin{array}{l}{∠BAC=∠DCA}\\{∠B=∠D}\\{∠B=∠D}\end{array}\right.$，
∴△ABC≌△CDA，
∴AD=BC，∠ACB=∠DAC，
∴AD∥BC．

点评 本题考查了三角形的全等的判定与性质，全等三角形的对应边相等，对应角相等．