题目内容
4．已知|a+1|+（b-2）2=0，则函数y=（b+3）x-a+b2-4b+4是什么函数？当x=-$\frac{1}{5}$时，函数值是多少？分析 根据非负数的性质求出a、b的值，从而得到函数的解析式，判断为一次函数；再将x=-$\frac{1}{5}$代入即可解答．
解答 解：∵|a+1|+（b-2）2=0，
∴a=-1，b=2，
∴y=5x+1+4-8+4=5x+1，
此函数为一次函数，当x=-$\frac{1}{5}$时，原式=5×（-$\frac{1}{5}$）+1=0．
点评 本题考查了非负数的性质和一次函数的定义，求出a、b的值是解题的关键．
练习册系列答案
相关题目
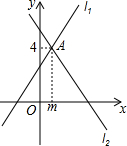如图，直线l1：y=x+3与直线l2：y=ax+b相交于点A（m，4）．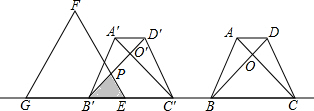
如图，按下列要求尺规作图：